w ist ein Versuch die Wurzel in C eindeutig zu definieren. Das Resultat von b) ist, dass die vorgeschlagene Definition an der Stelle 1 nicht stetig ist. Somit ist die Antwort auf c) dann Nein.
Nun mal zu b) ihr sucht ein z mit
|z-1| < ∂ und |w(z) - w(1)| >1
Da w(1) = 1 nach eurer Definition muss |w(z) - 1| >1 sein.
Betrag bedeutet Abstand in der komplexen Zahlenebene.
Deshalb hier mal eine Skizze.
|z-1|< ∂ heisst, dass wir in einer vorgegebenen Umgebung von 1 ein z suchen.
Du weisst, dass gemäss deiner Wurzeldefinition Winkel von 0 bis π rauskommen müssen.
Zahlen direkt unterhalb von 1 landen somit direkt oberhalb von -1 und sind sicher weiter als 1 von der Zahl 1 entfernt. Das gilt auch für alle Wurzeln aus komplexen Zahlen auf dem Einheitskreis in der unteren Halbebene.
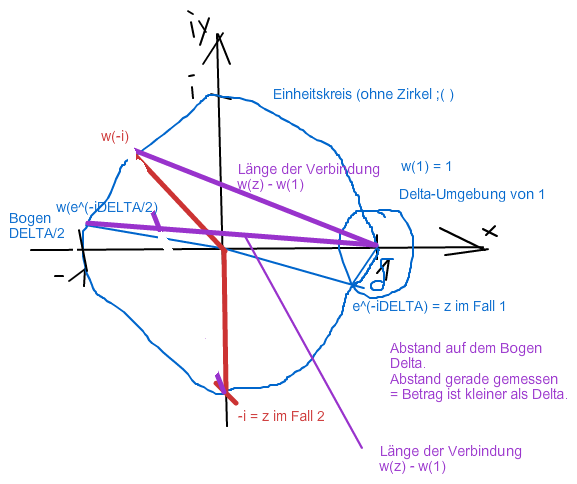
Mein Vorschlag für z
e^{-i∂} falls 0<∂<π/2
z:= {
-i = e^{-iπ/2} falls ∂≥ π/2
Da Winkel im Bogenmass genau die Bogenlänge auf dem Einheitskreis angeben, liegen die Zahlen e^{-i∂} sicher wie verlangt näher als ∂ bei 1.
Resultat dieser Teilaufgabe in Worten: In jeder noch so kleinen Umgebung der Zahl 1 gibt es eine Zahl, deren Wurzel mehr als 1 von w(1) entfernt ist. Es lässt sich also keine Umgebung finden, in der alle Zahlen eine Wurzel besitzen, die näher als ein kleiner vorgegebener Wert bei der Wurzel von 1 liegen. Deshalb ist w nicht stetig in 1.