Finde Teilmenge der Matrizen, die den Eigenwert 2 besitzen

Question

Betrachten wir den Unterraum W=span von

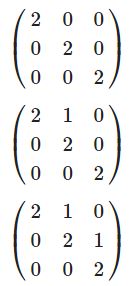
$\subset M_3(\mathbb{R})$

1.) Bestimme die Teilmenge $S\subset W$ der Matrizen, die die Zahl 2 als Eigenwert haben. Ist S ein Unterraum? Ein affiner Raum?

2.) Bestimmen sie die Matrizen in S, die diagonalisierbar sind?

3.) Bestimmen sie die Matrizen in S, die ähnlich zu einem elementaren Jordanblock sind.

Zu 1.) Ist nicht der ganze Unterraum W = S, weil ja alle Matrizen den Eigenwert 2 haben und dann als Vielfaches auch? Oder verstehe ich die Aufgabe nicht?

Answer 1

zu 1:

In dem Unterraum wäre aber auch  das 2 fache des ersten

und das ist

4     0     0
0     4     0
0      0     4

und das hat nur den Eigenwert 4,

gehört also nicht zu S.

Comments

Möglicherweise ist $S$ ein affiner Unterraum?

---

Hab ich auch schon gedacht.

Dann müssten die Differenzen zweier Matrizen aus W,

die beide den Eigenwert 2 haben, einen Untervektorraum

von W bilden.

---

Vielleicht $S=\begin{pmatrix}2&0&0\\0&2&0\\0&0&2\end{pmatrix}+\operatorname{span}\left\{\begin{pmatrix}0&1&0\\0&0&0\\0&0&0\end{pmatrix};\begin{pmatrix}0&1&0\\0&0&1\\0&0&0\end{pmatrix}\right\}$?