Hallo murphyxoo,
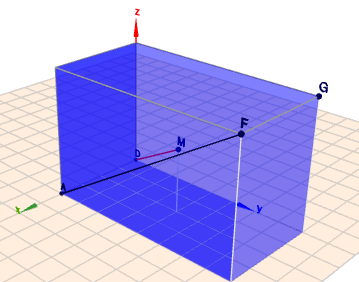
stelle Dir mal so einen Quader vor. So wie in dem Bild hier liegen alle Kanten parallel zu den Achse eine Koordinatensystems.
(wenn Du auf das Bild klickst, so kannst Du den Quader auch drehen)
unten links in der Ecke legt der Punkt \(A\) und oben rechts im Bild \(G\). Die Punkte \(A\) bis \(D\) liegen auf dem Boden (gegen den Uhrzeigersinn) und die Punkte \(E\) bis \(H\) bilden die Ecken der Deckfläche des Quaders. \(M\) wird wohl der Mittelpunkt des Quaders sein. Der Punkt \(B\) liegt bei \(B=(4;8;0)^T\). Weiter Koordinaten soltest Du mehr oder weniger ablesen können. \(D\), \(F\) und \(M\) habe ich noch eingezeichnet.
\(AF\) ist die Diagonale (schwarz) der Frontseite. \(DM\) die Verbindung (rot) vom Ursprung \(D\) zum Mittelpunkt \(M\). Die Längen berechnet man aus dem Betrag der Differenzen der Vektoren zu den einzelenen Punkten - es ist
$$|AF| = F -A = \left| \begin{pmatrix} 4\\ 8\\ 5\end{pmatrix} - \begin{pmatrix} 4\\ 0\\ 0\end{pmatrix} \right|= \left| \begin{pmatrix} 0\\ 8\\ 5\end{pmatrix} \right| = \sqrt{8^2+ 5^2}=\sqrt{89} \approx 9,4$$
$$|DM| = M-D= \left|\begin{pmatrix} 2\\ 4\\ 2,5\end{pmatrix} - \begin{pmatrix} 0\\ 0\\ 0\end{pmatrix}\right| = \left|\begin{pmatrix} 2\\ 4\\ 2,5\end{pmatrix}\right| = \sqrt{2^2+4^4+2,5^2} = \sqrt{26,25} \approx 5,1$$