Verfahren "wie?": (1,0) wählen, dann 2. Punkt, dann 3. Punkt (wie döschwo).
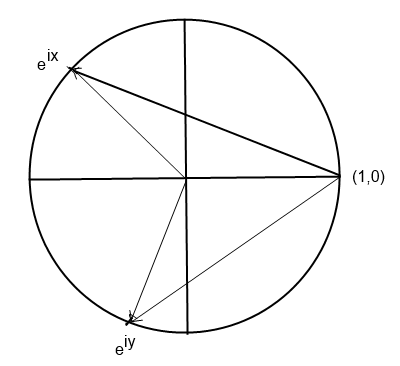
A(Dreieck)
= 1/2 * I (eix - e0) x ((eiy - e0) I
=1/2 * I [ \( \begin{pmatrix} cos x\\sin x\\0 \end{pmatrix} \) - \( \begin{pmatrix} 1\\0\\0 \end{pmatrix} \) ] x [\( \begin{pmatrix} cos y\\sin y\\0 \end{pmatrix} \) - \( \begin{pmatrix} 1\\0\\0 \end{pmatrix} \) ] I
= 1/2 * I \( \begin{pmatrix} cos x-1\\sin x\\0 \end{pmatrix} \) x \( \begin{pmatrix} cos y-1\\sin y\\0 \end{pmatrix} \) I
= 1/2 * I \( \begin{pmatrix}0\\0\\(cos x - 1)sin y - sin x (cos y - 1) \end{pmatrix} \) I
= 1/2 * I (cos x - 1)sin y - sin x (cos y - 1) I
Mittelwert(A(Dreieck))
= \( \frac{1}{2} \) * \( \frac{1}{2π*2π} \) \( \int\limits_{0}^{2π} \) \( \int\limits_{0}^{2π} \) I (cos x - 1)sin y - sin x (cos y - 1) I dx dy *) Nebenrechnung
= - \( \frac{1}{2} \) * \( \frac{1}{2π*2π} \) \( \int\limits_{0}^{2π} \) \( \int\limits_{y}^{2π} \)(cos x - 1)sin y - sin x (cos y - 1) dx dy
+ \( \frac{1}{2} \) * \( \frac{1}{2π*2π} \) \( \int\limits_{0}^{2π} \) \( \int\limits_{0}^{y} \)(cos x - 1)sin y - sin x (cos y - 1) dx dy
=\( \frac{1}{8π^{2}} \)[ \(\int\limits_{0}^{2π} \)\( \int\limits_{0}^{y} \)(cos x -1)sin y - sin x (cos y -1) dxdy - \( \int\limits_{0}^{2π} \)\( \int\limits_{y}^{2π} \)(cos x -1)sin y - sin x (cos y -1) dxdy]
= \( \frac{1}{8π^{2}} \) [ \( \int\limits_{0}^{2π} \) \( \int\limits_{0}^{y} \) sin(y - x) + sin(x) - sin(y) dx dy - \( \int\limits_{0}^{2π} \) \( \int\limits_{y}^{2π} \) sin(y - x) + sin(x) - sin(y) dx dy ]
= \( \frac{1}{8π^{2}} \) [\( \int\limits_{0}^{2π} \)[cos(y - x) - cos(x) - x sin(y) ] (0..y) dy - \( \int\limits_{0}^{2π} \)[cos(y - x) - cos(x) - x sin(y) ] (y..2π) dy]
= \( \frac{1}{8π^{2}} \) [ \( \int\limits_{0}^{2π} \) 1-cos(y) - y sin(y) -cos(y) +1 dy - \( \int\limits_{0}^{2π} \) cos(y) -1 -0 -1 + cos (y) +y sin(y) dy ]
= \( \frac{1}{8π^{2}} \) [ \( \int\limits_{0}^{2π} \) 2-2cos(y) - y sin(y) dy - \( \int\limits_{0}^{2π} \) 2cos(y) -2 +y sin(y) dy ]
= \( \frac{1}{4π^{2}} \) \( \int\limits_{0}^{2π} \) 2-2cos(y) - y sin(y) dy
= \( \frac{1}{4π^{2}} \) [ 2 y - 3 sin(y) + y cos(y) ] (0..2π)
= \( \frac{1}{4π^{2}} \) [ 4π + 2π ]
=1,5 / π
= 0,4774648 ....
Nebenrechnung:
(cos x - 1)sin y - sin x (cos y - 1)
= -sin(x - y) + sin(x) - sin(y)
= sin(y - x) + sin(x) - sin(y)
= 4 sin(x/2) sin(y/2) sin(y/2 - x/2) jeweils 4π-periodisch
≥0 für y≥x
{
<0 sonst