Transformieren einer Quadrik in Hauptachsenanlage

Question

Aufgabe:

Transformieren einer quadrik in hauptachsenanlage

Problem/Ansatz:

Funktion: x^2 − 2xy + y^2 + x − 3y − 4 = 0

wenn ich die matrix transformiere erhalte ich 2xy+2y^2 -3* wurzel(2) -4

lamda ist 0 und 2

D= (0,0,0,2)

T= 1/wurzel von 2 (1,1,-1,1)

(wenn ich mich nicht verrechnet habe!)

M (1I-9/4)

Würde gerne meine Rechnungen einfügen geht aber nicht !

Answer 1

Komme mit Deinen Angaben nicht klar?

Rechnen lassen mit allem Zwischen-Schritten

https://www.geogebra.org/m/jybmgrce

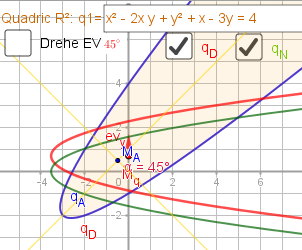
Nach dem Drehen (gemischte Glieder weg) ===>

\(\small q_D: \, 2 \; y^{2} - \sqrt{2} \; x - 2 \; \sqrt{2} \; y = 4\)

dann Translation mit

\(T \, :=  \,  \left\{ x = x, y = y + \frac{1}{2} \; \sqrt{2}, 1 \right\} \)

auf

\(M_q \, :=  \, \left(0, \frac{\sqrt{2}}{2} \right) , q_{N}: \, 2 \; y^{2} - \sqrt{2} \; x = 5\)

\(q_{N}: \, 2 \; x^{2} + \sqrt{2} \; y = 5\)

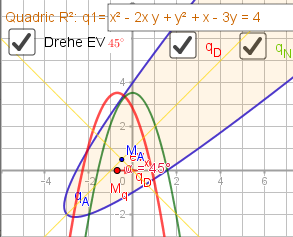
oder
\(q_{N}: \, 2 \; x^{2} - \sqrt{2} \; y = 5\)

Comments

sind denn meine Werte richtig?

---

Das weiß ich nicht

::matrix transformiere - was soll das sein?

::lamda ist 0 und 2 - richtig, wenn es die Eigenwerte sein sollen

D= (0,0,0,2) vermutlich richtig, wenn das die Diag sein soll

T= 1/wurzel von 2 (1,1,-1,1) - vermutlich richtig, wenn das die Drehmatrix sein soll:

Die HAT erfolgt durch eine Drehung (in achsenparallele Lage, d.h. gemischte Summanden der Quadrik (xy) sind weg ===> q_D siehe oben) und dann eine Verschiebung in Normallage)

---

Was meinst Du mit gemischte Glieder der quadrik? Welche soll ich da weg machen! Könntest du’s Bitte nachrechnen? Möchte wissen ob ich das richtig gerechnet habe!

Wie bekomme ich den Typ der normal Form heraus?!

---

Das findest Du alles auf der verlinkten Seite.....