Zeigen Sie lim(an)= a, n->inf ist äquivalent lim sup (an) = lim inf (an) = a, n->inf
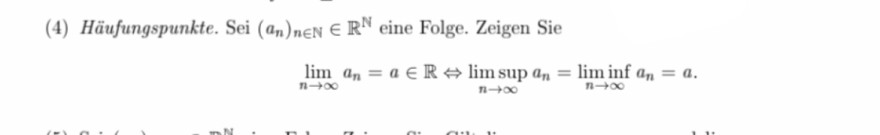
Text erkannt:
(4) Häufungspunkte. Sei (an)n∈N∈RN \left(a_{n}\right)_{n \in \mathbb{N}} \in \mathbb{R}^{\mathbb{N}} (an)n∈N∈RN eine Folge. Zeigen Sielimn→∞an=a∈R⇔lim supn→∞an=lim infn→∞an=a. \lim \limits_{n \rightarrow \infty} a_{n}=a \in \mathbb{R} \Leftrightarrow \limsup _{n \rightarrow \infty} a_{n}=\liminf _{n \rightarrow \infty} a_{n}=a . n→∞liman=a∈R⇔limsupn→∞an=liminfn→∞an=a.
Ein anderes Problem?
Willkommen bei der Mathelounge! Stell deine Frage einfach und kostenlos
