Hallo Babsi,
mit Spiegelmatrix
Der Fußpunkt \(F\) eines Punktes \(P\) auf eine Geraden durch \(A\) in Richtung des Vektors \(n\) berechnet sich aus$$F = A + \frac n{|n|} \cdot \left( \left(\frac n{|n|} \right)^T\cdot (P-A)\right) \\ \phantom{F} = \left[ \underline 1 - \frac 1{|n|^2} (n \cdot n^T)\right]A + \frac 1{|n|^2} (n \cdot n^T) \cdot P$$\(n \cdot n^T\) ist das dyadische Produkt. Die Spiegelung von \(P\) an der Geraden zum Spiegelpunkt \(P'\) ist dann die selbe wie die Spiegelung an \(F\) - also$$\begin{aligned} P' &= 2F - P \\ &= 2\left[ \underline 1 - \frac 1{|n|^2} (n \cdot n^T)\right]A + \left[\frac 2{|n|^2} (n \cdot n^T) - \underline 1\right] P \end{aligned}$$So ist es eine affine Abbildung. Um daraus eine lineare(!) Abbildung zu machen müsste man zu homogene Koordinaten übergehen.
Hier ist also$$A = \begin{pmatrix}1\\ -1\\ 0\end{pmatrix}, \quad n = \begin{pmatrix}4\\ 4\\ 1\end{pmatrix}, \quad P = \begin{pmatrix}6\\ 4\\ -7\end{pmatrix} \\ P' = \begin{pmatrix}2\\ -2\\ 0\end{pmatrix} + \frac 1{33}\begin{pmatrix}-1& 32& 8\\ 32& -1& 8\\ 8& 8& -31\end{pmatrix} P \\ \phantom{P'} = \begin{pmatrix}2\\ -2\\ 0\end{pmatrix} + \begin{pmatrix}2\\ 4\\ 9\end{pmatrix} = \begin{pmatrix}4\\ 2\\ 9\end{pmatrix}$$womit die X-Koordinate weder 2, 6 oder 7 ist. Nun deutet aber die Aussage
Sei S die lineare Abbildung,...
.. darauf hin, dass mit 'Gerade' die Ursprungsgerade in Richtung \(n\) gemeint ist und dass das \(a\) für diesen Aufgabenteil irrelevant ist. Dann entfällt der konstante Anteil und \(P'\) ist $$P' = \begin{pmatrix}2\\ 4\\ 9\end{pmatrix}, \quad \implies p_x' = 2$$und die Spiegelmatrix ist$$S = \frac 1{33}\begin{pmatrix}-1& 32& 8\\ 32& -1& 8\\ 8& 8& -31\end{pmatrix}, \quad P' = S \cdot P $$anbei ein Bildchen mit beiden Lösungen
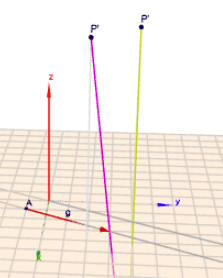
(klick auf das Bild)
Nachtrag:
Welche x Koordinaten besitzt das Bild des Vektors (6,4,-7)?
2, 6 oder 7
man kann diese Frage auch ohne Rechnung beantworten, wenn man sich die Ursprungsgerade und den Punkt \(P\) räumlich vorstellt (s.Bild). Dann muss nämlich die X-Koordinate des Bildes kleiner sein, als die von \(P\). Und damit kommt von den drei Auswahlmöglichkeiten nur \(p_x'=2\) in Frage!