Hallo bazinga, bin wieder da :-)
Gegenstände in Quaderform (Breite x Länge x Höhe, alles rechte Winkel) gibt es unzählige, zum Beispiel
Taschenbücher, Zigarettenschachteln, Computergehäuse, Tetra-Pack Kaffeemilch usw.
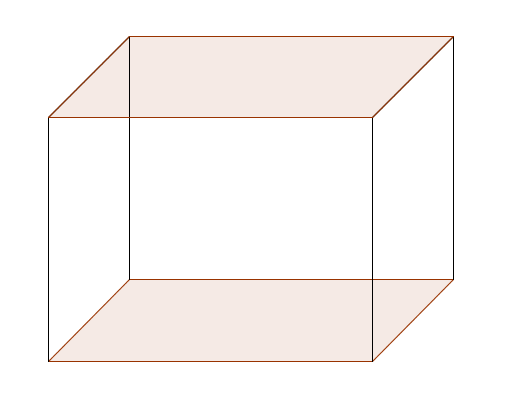
Wenn Du sie Dir ansiehst, stellst Du fest, dass jeweils zwei sich gegenüberliegende Seiten gleich sind (im obigen Bild zum Beispiel "Boden" und "Decke"); sie haben also jeweils die Fläche a * b (bwz. a * c bzw. b * c); so kommen wir insgesamt auf 6 Seiten mit der Gesamtfläche A =
2 * Breite * Länge +
2 * Breite * Höhe +
2 * Länge * Höhe
Ich habe einfach die gegebenen Maße in diese Summenformel eingesetzt und ein wenig multipliziert und addiert :-)
Zur Raumdiagonale des Quaders 1:
Wir nehmen zum Beispiel die von "vorne-unten-links" nach "hinten-oben-rechts"
Dazu nutzen wir, weil wir mit rechtwinkligen Dreiecken arbeiten, den Satz des Pythagoras a2 + b2 = c2
Die Diagonale des Bodens ist c = √(a2 + b2).
Diese wird im neuen rechtwinkligen Dreieck zu einer der Katheten, die andere ist die Höhe des Quaders.
Die gesuchte Raumdiagonale ist dann
d = √(c2 + h2) wobei h die Höhe des Quaders ist.
Also haben wir insgesamt
d = √[(a2 + b2) + h2]
Mit
a = 7,5cm; b = 3,2cm; c = 5cm (hier "h") sollte sich ergeben:
d = √[(7,52 + 3,22) + 52] ≈ 9,565
Ich hoffe, ich habe keinen Fehler gemacht :-)
Aber das prinzipielle Vorgehen sollte klar geworden sein, nicht wahr?
Besten Gruß