Wie geht das?
Oswald schrieb:
Bestimme \(r\) so dass der Vektor von (2|1|0)+r(4|1|0) zu P senkrecht zum Richtungsvektor der Geraden ist.
wenn die beiden Vektoren \(\vec d\) und \(P - g(r)\) senkrecht zu einander stehen, dann muss ihr Skalarprodukt =0 sein, also$$\vec d= \begin{pmatrix}4\\ 1\\ 0\end{pmatrix}, \quad g: \space \vec x = \begin{pmatrix}2\\ 1\\ 0\end{pmatrix} + r \begin{pmatrix}4 \\ 1\\ 0\end{pmatrix}, \quad P = \begin{pmatrix}8\\ 11\\ 0\end{pmatrix}\\ \begin{aligned} \vec d \cdot (P - g(r))&= 0 \\ \begin{pmatrix}4\\ 1\\ 0\end{pmatrix}\cdot\left(\begin{pmatrix}8\\ 11\\ 0\end{pmatrix} - \begin{pmatrix}2\\ 1\\ 0\end{pmatrix} - r \begin{pmatrix}4 \\ 1\\ 0\end{pmatrix}\right) &= 0\\ \begin{pmatrix}4\\ 1\\ 0\end{pmatrix}\cdot\left(\begin{pmatrix}6\\ 10\\ 0\end{pmatrix} - r \begin{pmatrix}4 \\ 1\\ 0\end{pmatrix}\right) &= 0 \\ 34 - 17r &= 0 \\\implies r &= 2\end{aligned}$$
Setze den Wert in die Geradengleichung ein um einen Punkt R der Geraden zu bestimmen.
\(R\) ist der Fußpunkt bzw. die Projektion von \(P\) auf die Gerade \(g\):$$R = g(2) = \begin{pmatrix}2\\ 1\\ 0\end{pmatrix} + 2\cdot \begin{pmatrix}4\\ 1\\ 0\end{pmatrix} = \begin{pmatrix}10\\ 3\\ 0\end{pmatrix}$$
Abstand von Punkt und Gerade ist der Abstand von P zu R
$$|RP| = |P - R| = \left| \begin{pmatrix}8\\ 11\\ 0\end{pmatrix} - \begin{pmatrix}10\\ 3\\ 0\end{pmatrix} \right| = \sqrt{68}$$
.. und am besten machst Du Dir eine Skizze, was hier einfach ist, da sich alles in der XY-Ebene abspielt:
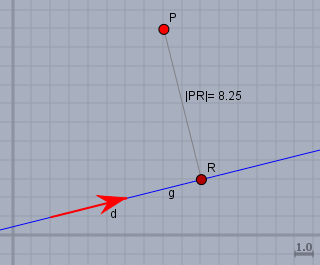
und hier kann man auch das Ergebnis schön überprüfen!