Zunächst einmal du eine Funktion A(x), welche die Querschnittsfläche beschreibt konstruieren.
Ich verstehe die Aufgabe so, dass du dies einmal für eine Rechtecks- und Dreieckspyramide machen sollst.
Zunächst ist die Formel für die jeweiligen Grundflächen: Rechtecksfläche AR = a*b , gleichseitiges Dreieck $$A_D= \frac{\sqrt{3}}{4}*a^2$$
1)
Nun hängen diese Fläche natürlich von der Höhe x des Querschnitts ab, also AR(x)= a(x)*b(x) beim Rechteck, gleichseitiges Dreieck $$A_D(x)= \frac{\sqrt{3}}{4}*a(x)^2$$
Es ist klar, dass diese Flächen jeweils kleiner mit wachsender Höhe werden müssen, zu dem ist von einem linearen Abfall auszugehen, da die Pyramide gleichmäßig schmaler wird.
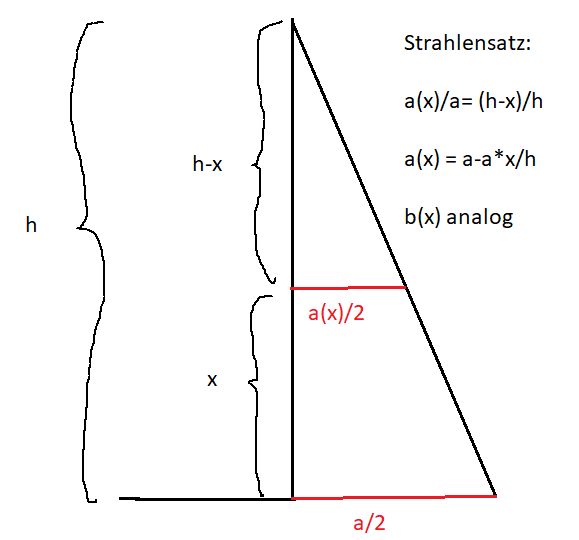
In $$ A_R(x)=a*b*(1-x/h)^2 $$ und $$ A_D(x)=\frac{\sqrt{3}}{4} a^2(1-x/h)^2 $$ einsetzen.
2) Diese Querschnitte kann man als infinitesimal dünne "Scheiben" mit der Dicke dx betrachten, so dass das Volumen einer Scheibe durch A(x)*dx gegeben ist.
$$V_R=ab\int \limits_{0}^{h}(1-\frac{x}{h})^2dx=ab\frac{\text{h}}{3}$$
$$V_D=\frac{\sqrt{3}}{4} a^2\int \limits_{0}^{h}(1-\frac{x}{h})^2dx=\frac{\sqrt{3}}{4} a^2 \frac{\text{h}}{3}$$
3) Formelsammlung
PS: In meiner Vorschau wird der Latex-Text teiwleise nicht richtig angezegit, hoffe dass sieht nach dem posten anders aus, ansonsten Stellen kopieren und einfügen:
https://www.matheretter.de/rechner/latex