Anhand des Wendepunktes Funktionsgleichung ermitteln

Question

Aufgabe:

Gegeben ist eine ganzrationale Funktion / vierten Grades, deren Graph symmetrisch zur y-Achse ist und durch den Ursprung des Koordinatensystems verläuft. Der Punkt W (1/-0,625)ist ein Wendepunkt des Graphen von f. Anhand dieser Angaben kann eine Funktionsgleichung von f ermittelt werden. Ermitteln Sie eine Funktionsgleichung von f

Problem/Ansatz:

Ich habe versucht die Gleichung der Fkt f zu ermittlen, doch hat es nicht geklappt. Ich bitte um Hilfe

Answer 1

Gegeben ist eine ganzrationale Funktion / vierten Grades,

$f(x) = ax^4 + bx^3 + cx^2 + dx + e$

deren Graph symmetrisch zur y-Achse ist

(1)        $b = 0$

(2)        $d = 0$

und durch den Ursprung des Koordinatensystems verläuft.

(3)        $f(0) = 0$

Der Punkt W (1/-0,625)

(4)        $f(1) = -0{,}625$

ist ein Wendepunkt des Graphen von f

(5)        $f''(1) = 0$

Löse das Gleichungssystem aus diesen fünf Gleichungen.

Answer 2

Aloha :)

Willkommen in der Mathelounge... \o/

Wir suchen eine ganzrationale Funktion vierten Grades$$f(x)=ax^4+bx^3+cx^2+dx+e$$deren Graph symmetrisch zur $y$-Achse ist$$f(x)=ax^4+\cancel{bx^3}+cx^2+\cancel{dx}+e=ax^4+cx^2+e$$und durch den Ursprung des Koordinatensystems verläuft$$f(x)=ax^4+cx^2+\cancel{e}=ax^4+cx^2$$

Der Punkt $W(1|-\frac58)$ ist ein Wendepunkt der Graphen, das heißt:

(1) Der Punkt selbst liegt auf dem Graphen:$$-\frac58=f(1)=a+c$$

(2) Die zweite Ableitung verschwindet bei $x=1$:$$f'(x)=4ax^3+2cx\quad;\quad f''(x)=12ax^2+2c\quad;\quad 0\stackrel!=f''(1)=12a+2c$$Wir haben also zwei Gleichungen für die unbekannten Parameter:$$a+c=-\frac58\quad;\quad 6a+c=0\implies$$$$(6a+c)-(a+c)=0-\left(-\frac58\right)\implies$$$$5a=\frac58\implies a=\frac18$$

Wegen $c=-\frac58-a=-\frac58-\frac18=-\frac34$ lautet die gesuchte Funktionsgleichung:$$f(x)=\frac18x^4-\frac34x^2$$

Plotlux öffnen

f₁(x) = 1/8·x⁴-3/4·x²P(1|-5/8)Zoom: x(-4…4) y(-2…4)

Answer 3

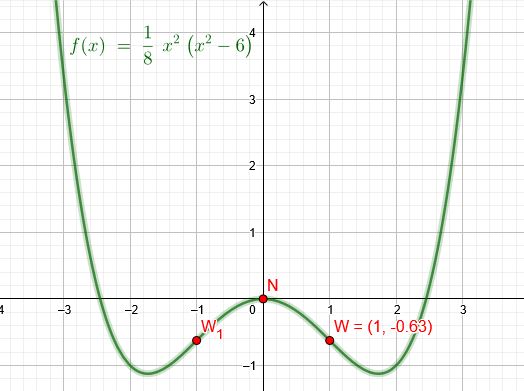
"Gegeben ist eine ganzrationale Funktion / vierten Grades, deren Graph symmetrisch zur y-Achse ist und durch den Ursprung des Koordinatensystems verläuft. Der Punkt $W (1|-0,625)$ist ein Wendepunkt des Graphen von f. Anhand dieser Angaben kann eine Funktionsgleichung von f ermittelt werden. Ermitteln Sie eine Funktionsgleichung von f."

Weg über die Nullstellenform der Parabel 4. Grades:

$W (1|-0,625)$ ist Wendpunkt. Somit liegt wegen der Achsensymmetrie der 2.Wendepunkt bei  $W_1 (-1|-0,625)$

Der Graph von f geht durch den Punkt $N(0|0)$.Insofern ist bei N eine doppelte Nullstelle.

$f(x)=a*x^2*(x-N)*(x+N)=ax^2*(x^2-N^2)=a*x^4-ax^2*N^2$

$W (1|-0,625)$

1.)$f(1)=a*1^4-a*1^2*N^2=a-a*N^2=-0,625$

$W (1|....)$

$f´(x)=4*a*x^3-2*a*x*N^2$

$f´´(x)=12*a*x^2-2*a*N^2$

2.)$f´´(1)=12*a*1^2-2*a*N^2=0$  →  $N^2=6$ →$N_1=\sqrt{6}$ ∨ $N_2=-\sqrt{6}$

$N^2=6$ ∈  1.) $a-a*6=-0,625$ →$a=\frac{0,625}{5}=\frac{1}{8}$

$f(x)=\frac{1}{8}*x^2*(x^2-6)$