Wie prüfe ich ob ein bestimmter Vektor ein Fundamentalsystem eines DGL- Systems ist?

Question

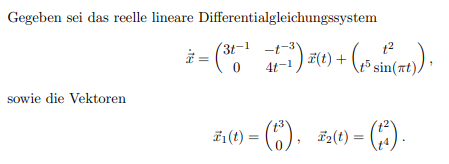
Text erkannt:

Gegeben sei das reelle lineare Differentialgleichungssystem
\( \dot{\vec{x}}=\left(\begin{array}{cc} 3 t^{-1} & -t^{-3} \\ 0 & 4 t^{-1} \end{array}\right) \vec{x}(t)+\left(\begin{array}{c} t^{2} \\ t^{5} \sin (\pi t) \end{array}\right) \text {, } \)
sowie die Vektoren
\( \vec{x}_{1}(t)=\left(\begin{array}{c} t^{3} \\ 0 \end{array}\right), \quad \vec{x}_{2}(t)=\left(\begin{array}{c} t^{2} \\ t^{4} \end{array}\right) \)

Ich soll herausfinden ob die angegebenen Vektoren ein Fundamentalsystem für das gegebene DGL-System ist. Ich kenne das nur mit Konstanten in einer anderen Form und habe nichts gefunden bezüglich Variablen und einem DGL-System das so aussieht. Wie muss ich auf so eine Aufgabe herangehen? Ich stehe hier echt auf dem Schlauch

Vielen Dank im voraus.

Answer 1

Hallo,

Betrachte den homogenen Teil:

x1=t^3 +t^2

x1'=3t^2 +2t

x2=t^4

x2'=4t^3

--->einsetzen in:

x1'= (3/t) x1 -(1/t^3)x2

3t^2 +2t =3t^2+3t -t

3t^2 +2t =3t^2+2t ->stimmt

------------------------------------

x2'= (4/t) x2

4t^3=(4/t)  *t^4

4t^3= 4t^3 ->stimmt

Comments

Oh wow. Ich hab da wohl sehr kompliziert gedacht. Viel einfacher als erwartet, vielen dank