Zum Verständnis: Die "Eckpunkte" sind die drei Dreieckspunkte A, B, C.
Eine Mittelsenkrechte ist jeweils die Gerade, die eine Dreiecksseite halbiert und senkrecht auf ihr steht:
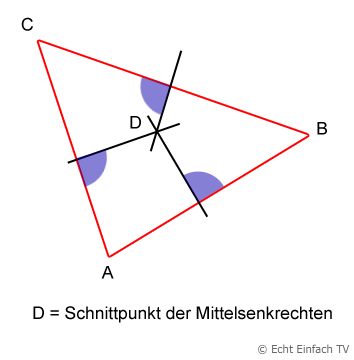
Du musst also jetzt die oben nicht eingezeichneten Strecken ausrechnen: AD, BD und CD.
Dein jeweiligen Punkt auf der Mitte (dort wo die Senkrechte anfängt, auch Seitenmittelpunkt genannt) errechnest du, indem du für Bsp Strecke AB die Koordinaten von A nimmst und von B und jeweils halbierst:
A (-1 | -2)
B (4 | -1)
x: (-1 + 4) / 2 = 1,5
y: (-2 + (-1) / 2 = -1,5 -> PunktAB/2 (1,5 | -1,5)
Diese Punkte benötigst du zur Berechnung, denn du berechnest von ihnen aus die Steigung der Mittelsenkrechten.
Wenn du nun Funktionsgleichungen f(x)=m*x + n bildest für alle 3 Mittelsenkrechten, dann schneiden sie sich alle in 1 Punkt. Die Koordinaten dieses Punktes brauchst du. Sobald du diese hast, sind die Abstände von Punkt zu Punkt trivial per Subtraktion zu berechnen.
Eingermaßen verstanden?