Im Zusammenhang mit meinen Artikeln zum Einsatz digitaler Werkzeuge beim Lehren und Lernen von Mathematik wurde bemängelt, dass Verbesserungsvorschläge fehlen - deshalb folgen hier zwei Vorschläge.
Vorausschicken muss man allerdings, dass man bei Durchsicht der Lehrpläne (auch des Gymnasiums) feststellt, dass die verbindlichen Unterrichtsinhalte sehr arm an Themen sind, die ohne CAS gar nicht zu bewältigen sind. Für den meisten Lösungen angebotener Aufgaben genügt ein moderater Taschenrechnereinsatz und bei etwas Übung im Kopfrechnen benötigt man in vielen Fällen gar kein digitales Werkzeug zur Problemlösung. Aufgabenvorschläge, die einen CAS-Einsatz nahelegen oder diesen sogar fordern, findet man in der didaktischen Fachliteratur, in ministeriellen Vorgaben und inzwischen auch in Unterrichtswerken. Nicht selten ist die Begründung für den Einsatz digitaler Algebra die damit verbundene Zeitersparnis. Leider fällt die angestrebte Zeitersparnis meist recht marginal aus. Schon die Rückkehr zu früheren Formen der Aufgabenstellung ohne umfangreiche Texte voller Distraktoren würde zu einem deutlich höheren Zeitgewinn führen.
Exemplarisch soll hier zunächst eine Aufgabe genannt werden, welche den CAS-Einsatz rechtfertigt, weil eine Lösungsidee möglicherweise erst nach umfangreichen Darstellungen im Koordinatensystem entsteht:
Die Geraden PQ mit P(a|a2), Q(-b|b2) und a≠b schneiden für alle natürlichen Zahlenpaare (a|b) mit a≠1 und b≠1 die y-Achse. Welche natürlichen Werte nennen nicht den y-Achsenabschnitt einer Geraden PQ? Welche Geraden PQ verlaufen parallel zur x-Achse?
Mit CAS erhält man diese Darstellung:

Die hypothetischen Antworten auf die gestellten Fragen können in dieser Darstellung abgelesen werden:
1. Die natürlichen Werte, welche nicht y-Achsenabschnitt einer Geraden PQ sind, sind genau die Primzahlen.
2. Die natürlichen Werte, durch welche Geraden PQ parallel zur x-Achse verlaufen, sind die Quadratzahlen (außer 1).
Die Aufgabe hat - gemessen an heutigen Forderungen – zwei fundamentale Mängel: Sie hat keinen Bezug zu irgendeiner lebensweltlichen Anwendung und sie behandelt elementare Zahlentheorie, welche seit einigen Jahrzehnten nicht mehr Unterrichtsthema ist. Aber im Zuge der Bewältigung dieser Aufgabe erleben SuS, wie mathematisches Wissen gewonnen werden kann. Hier wird auf der Basis gewisser Vorkenntnisse eine selbständige Entdeckung gemacht, die dann noch zu beweisen ist.
Der Einsatz von DGS im Mathematikunterricht wird in vielen vorgeschlagenen Fällen ähnlich unzutreffend mit dem Argument des Zeitgewinns begründet. Klassische Konstruktionen mit Zirkel und Lineal können aber vor allem dann zeitsparender mit DGS durchgeführt werden, wenn Invarianten bei Variation der Konstruktionsfigur zu entdecken sind. Die Beweisidee zum Nachweis der Invarianz ist oft eng mit ihrer Entdeckung verbunden. Dazu eine Beispielaufgabe:
Zwei Kreise K1 und K2 schneiden sich in P und C. Eine Gerade g durch P scheide den kleineren Kreis K1 auf dem kürzesten Bogen (CP) in B und den größeren Kreis K2 auf dem längsten Bogen (CP) in A. Was kann über alle so konstruierten Dreiecke ABC ausgesagt werden?
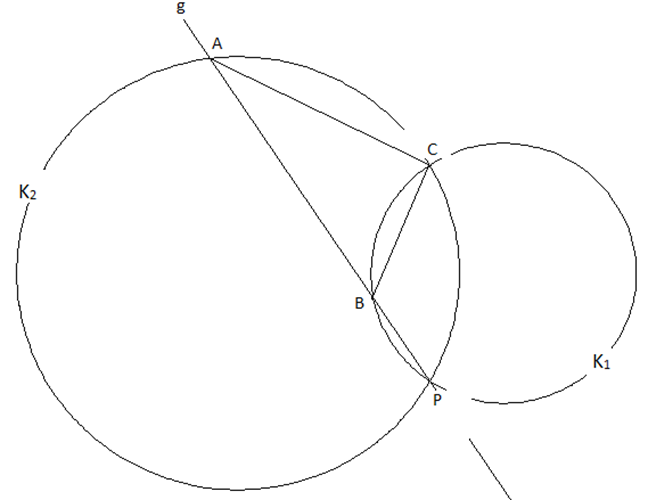
Auch hier wird erlebbar gemacht, wie mathematisches Wissen gewonnen wird. Eine selbständige Entdeckung liefert die anschließend erforderliche Beweisidee gleich mit. Im Zuge des Beweises wird ein weiterer Ähnlichkeitssatz entwickelt: Dreiecke sind ähnlich, wenn sie in der Größe eines Innenwinkels und der Größe des gegenüberliegenden Nebenwinkels übereinstimmen.
Auch diese Aufgabe hat keinerlei Bezug zu Anwendungen in der Lebenswelt. Es sieht danach aus, als könnte der Verzicht auf das Paradigma des Anwendungsbezugs eine Flut von Gelegenheiten nach sich ziehen, Aufgaben zu finden, die den Einsatz von CAS und DGS rechtfertigen.