Grenzen bei der Substitution

Question

Ich habe ein Verständnisproblem zu den Grenzen bei der Substitution. Ich dachte man muss die alten Grenzen in u einsetzen und hat dann neue Grenzen mit denen man weiter rechnet. Wie zum Beispiel hier:

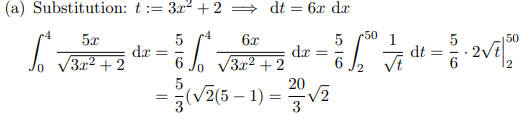
Text erkannt:

(a) Substitution: $t:=3 x^{2}+2 \Longrightarrow \mathrm{d} t=6 x \mathrm{~d} x$
$\begin{aligned} \int \limits_{0}^{4} \frac{5 x}{\sqrt{3 x^{2}+2}} \mathrm{~d} x & =\frac{5}{6} \int \limits_{0}^{4} \frac{6 x}{\sqrt{3 x^{2}+2}} \mathrm{~d} x=\frac{5}{6} \int \limits_{2}^{50} \frac{1}{\sqrt{t}} \mathrm{~d} t=\left.\frac{5}{6} \cdot 2 \sqrt{t}\right|_{2} ^{50} \\ & =\frac{5}{3}\left(\sqrt{2}(5-1)=\frac{20}{3} \sqrt{2}\right. \end{aligned}$

Hier werden ja offensichtlich 4 und 0 in t eingesetzt und die neuen Grenzen 50 und 2 entstehen.

Bei folgender Aufgabe jedoch:

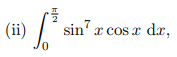
Text erkannt:

(ii) $\int \limits_{0}^{\frac{\pi}{2}} \sin ^{7} x \cos x \mathrm{~d} x$,

Wurde die Stammfunktion 1/8 sin ⁸ x gebildet und dann für x PI/2 und 0 eingesetzt, also die alten Grenzen. Ich hätte jetzt vermutet, dass wir die alten Grenzen in u einsetzen, also hier in sin x und 1 und 0 erhalten und das dann in die Stammfunktion einsetzen. Das wurde in der Lösung die mir vorliegt jedoch so nicht gemacht, sondern es wurde Pi/2 und 0 eingesetzt wodurch dann 1/8 - 0 zustande kam. Kann mir das jemand erklären?

Comments

vgl:

https://www.integralrechner.de/

Answer 1

Aloha :)

Du musst die substituierten Integrationsgrenzen nur verwenden, wenn in dem Ergebnis weiterhin die substituierte Variable vorkommt. In deinem ersten Beispiel ist das Ergebnis mit der substituierten Variablen $t$ angegeben, also müssen da die Grenzen für $t$ eingesetzt werden.

Bei dem von dir genannten zweiten Integral, taucht im Ergebnis wieder die ursprüngliche Integrationsvariable $x$ auf. Daher musst du dort auch die Grenzen für $x$ einsetzen.

Comments

Vielen Dank!

Answer 2

Wenn du die Substitution rücksubstituierst, dann musst du die alten Grenzen einsetzen. Wenn man sich das Rücksubstituieren spart, dann kann man auch die umgerechneten Grenzen einsetzen.

$$\int \limits_{0}^{\frac{\pi}{2}} \sin^{7} x \cos x ~dx \newline \text{Subst. u = sin x ; du/dx = cos x} \newline = \int \limits_{0}^{1} u^{7} ~du \newline = \frac{1}{8} \cdot u^8 |_0^1 \newline = \frac{1}{8}$$

Comments

Alles klar, danke.

Answer 3

Hallo,

hab die 2.Aufgabe mal nach 2 Wegen berechnet: