Aufgabe:
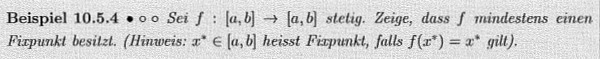
Text erkannt:
Fixpunkt besitzl. (Hinweis: \( x^{*} \in[a, b] \) heisst Fixpunkt, falls \( f\left(x^{*}\right)=x^{*} \) gilt).
Problem/Ansatz:

Text erkannt:
Lösung: Anstatt \( f \) selbst zu betrachten, betrachten wir eine Hilfsfunktion. Das Aufstellen einer Hilfsfunktion ist eine übliche Praxis bei der Lösung solcher Aufgaben. Die Form dieser Hilfsfunktion wird oft vom Kontext suggeriert. In diesem Fall betrachten wir die folgende Hilfsfunktion
\( h(x)=f(x)-x . \)
\( h \) erlaubt es, die Bedingung eines Fixpunktes \( f(x)=x \) auf ein Nullstellenproblem \( h(x)=f(x)-x= \) 0 zu transformieren. Da \( f \) und die Funktion \( x \) auf \( [a, b] \) stetig sind, ist auch \( h \) auf \( [a, b] \) stetig (weil Differenz zweier stetiger Funktionen). Nun werten wir \( h \) an den Stellen \( x=a \) und \( x=b \) aus. Einerseits gilt
\( h(a)=f(a)-a \stackrel{f(a) \geq a}{\geq} 0, \)
weil \( f(a) \in[a, b] \). Andererseits gilt
\( h(b)=f(b)-b \stackrel{f(b) \leq b}{\leq} 0 . \)
Nach dem Zwischenwertsatz gibt es also ein \( x^{*} \in[a, b] \), sodass \( h\left(x^{*}\right)=0 \). Das impliziert \( h\left(x^{*}\right)= \) \( f\left(x^{*}\right)-x^{*}=0 \), also \( f\left(x^{*}\right)=x^{*}, x^{*} \) ist somit der gesuchte Fixpunkt.