Bestimmen Sie einen Funktionsterm f(x) für den rechts abgebildeten Kanalboden.

Question

Für Freizeitaktivitäten im Wassersport wird ein neuer Kanal als Verbindung zwischen zwei Seen angelegt.
a) Bestimmen Sie einen Funktionsterm $f(x)$ für den rechts abgebildeten Kanalboden.
b) Berechnen Sie den Flächeninhalt der abgebildeten Querschnittsfläche des Kanals.

c) Verwenden Sie die Funktion f, die den Kanalboden beschreibt, und betrachten Sie den um zwei Einheiten nach unten verschobenen Graphen der Funktion $g$ mit $g(x)=f(x)-2$. Die x-Achse beschreibt nun die Wasseroberfläche. Berechnen Sie mithilfe der Funktion g den Flächeninhalt der Querschnittsfläche.
d) Der Kanal hat eine Gesamtlänge von einem Kilometer. Berechnen Sie das Wasservolumen.
e) Im Sommer steht das Wasser im Kanal an der tiefsten Stelle $1 \mathrm{~m}$ hoch. Bestimmen Sie das Wasservolumen des beschriebenen Kanals im Sommer.

Comments

Willst Du den Kanalboden als Kreisbogen oder als Parabel oder als etwas anderes beschrieben haben?

---

a) Bestimmen Sie einen Funktionsterm $f(x)$ für den rechts abgebildeten Kanalboden.

Ist das keine klare Ansage?

---

Nutze die Symmetrie und verwende die Punkte (0|0) und (4|2).

Rot: Parabel

Grün: Kreis

---

Ist das keine klare Ansage?

Ich habe nicht behauptet, es sei keine klare Ansage. Sondern ich habe eine klare Frage gestellt. An den Fragesteller, nach seinen Präferenzen. Denn Kreis und Parabel und auch bspw. Kettenlinie sind hier nicht so wahnsinnig unterschiedlich:

Answer 1

a) Bestimmen Sie einen Funktionsterm $f(x)$ für den abgebildeten Kanalboden.

Scheitelpunktform der Parabel

$f(x)=a \cdot (x-x_S)^2+y_S$

Scheitel bei $S(0|0)$

$f(x)=a \cdot (x)^2$

$P(4|2)$:     $f(4)=a \cdot 4^2=16a=2$     $a=\frac{1}{8}$ 

$f(x)=\frac{1}{8} \cdot x^2$

b) Berechnen Sie den Flächeninhalt der abgebildeten Querschnittsfläche des Kanals.

$A= 2 \cdot \frac{1}{8} \cdot\int\limits_{0}^{4} x^2 dx=[\frac{x^3}{3}]_{0}^{4}=[\frac{64}{3}]-[0]$

$A= \frac{1}{4} \cdot\int\limits_{0}^{4} x^2 dx=[\frac{x^3}{3}]_{0}^{4}=[\frac{64}{3}]-[0]$
$4A= \int\limits_{0}^{4} x^2 dx=[\frac{x^3}{3}]_{0}^{4}=[\frac{64}{3}]-[0]$

$A=\frac{16}{3} m^{2}$

c) Verwenden Sie die Funktion f, die den Kanalboden beschreibt, und betrachten Sie den um zwei Einheiten nach unten verschobenen Graphen der Funktion $g$ mit $g(x)=f(x)-2$. Die x-Achse beschreibt nun die Wasseroberfläche. Berechnen Sie mithilfe der Funktion g den Flächeninhalt der Querschnittsfläche.

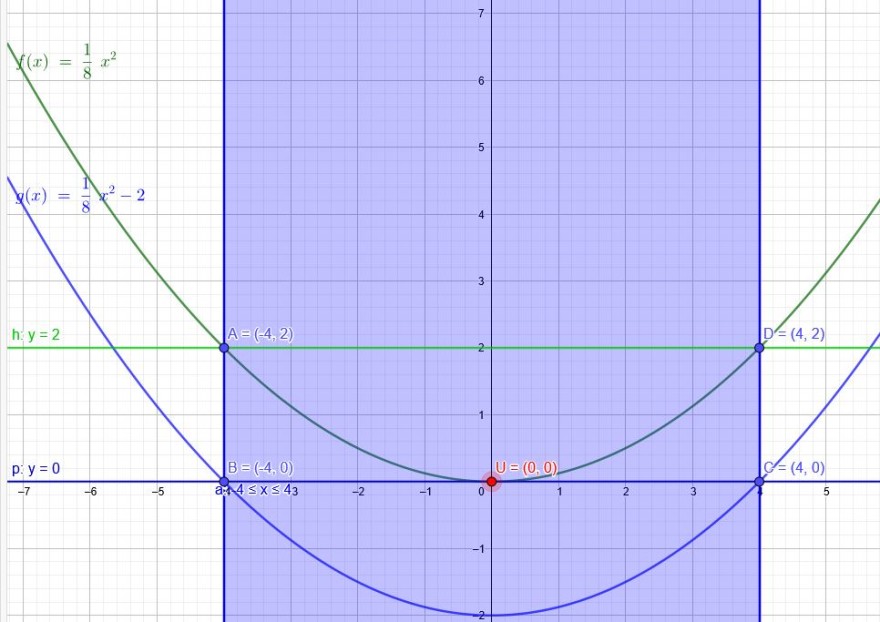
Die Flächenstücke unter der Parabel A,B und U sowie U,C und D sind zusammen  $A=\frac{16}{3} m^{2}$ groß.

Das Rechteck A, B,C und D ist $8\cdot 2=16m^{2}$ groß.

Somit ist die gesuchte Fläche $A=16m^{2}-\frac{16}{3} m^{2}=\frac{32}{3}m^{2}$ groß.