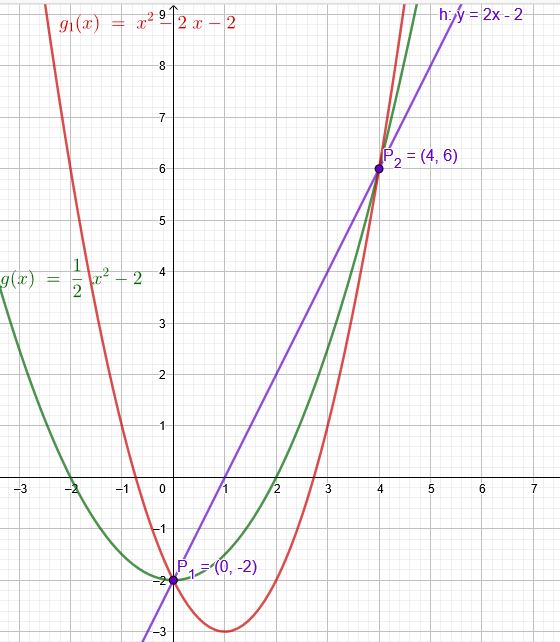
\( y=\frac{1}{2} x^{2}-2 \) \( \mathrm{y}=\mathrm{x}^{2}-2 \mathrm{x}-2 \)
\( \frac{1}{2} x^{2}-2=\mathrm{x}^{2}-2 \mathrm{x}-2 \)
\( \frac{1}{2} x^{2}=x^2-2x \)
\( x^{2}-4x=0 \) Satz vom Nullprodukt:
\( x_1=0\) \( y(0)=-2 \)
\( x_2=4\) \( y(4)=6 \)
Geradengleichung:
\( \frac{y+2}{x-0}=\frac{6+2}{4-0} \)
\( \frac{y+2}{x}=\frac{8}{4}=2 \)
\( y=2x-2 \)