Ein gleichseitiges Dreieck ABC der Seitenlänge a wird durch Kreisbögen um seine Eckpunkte mit dem Radius a zu einem Reuleaux-Dreieck ergänzt und durch die Verbindung seiner Seitenmitten D, E und F in 4 kongruente Teile zerlegt.
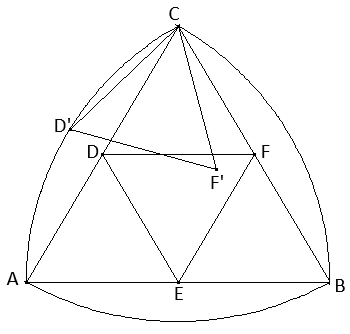
Das Teildreieck DFC wird um C so gedreht, dass D als Bildpunkt D' auf dem Rand des Reuleaux-Dreiecks liegt. In welchem Verhältnis teilt DF die Strecke |\( \overline{D'F'} \)?