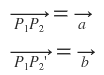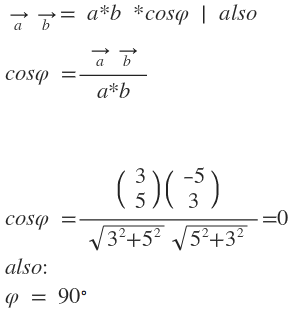Im Dreidimensionalen müsstest du Drehung um einen Punkt etwas genauer beschreiben. Die Richtung der Drehung ist erst bei einer Drehachse wirklich vorgegeben. Ohne diese Vorgabe lieget der Bildpunkt irgendwo auf einem Kreis, der senkrecht zur durch die beiden Punkten vorgegebenen Achse liegt.
Ist die Drehung aber mit Winkel und Rotationsachse vorgegeben kann man auch mit sog. Rotationsmatrizen arbeiten.
Im Zweidimensionalen kannst du auch mit komplexen Zahlen oder mit Matrizen Drehungen um den Koordinatenursprung darstellen.
Du benutzt hier eine Eigenschaft der Multiplikation von komplexen Zahlen: Winkel werden addiert, Radien multipliziert. Multiplikation mit einer komplexen Zahl a ≠0 beschreibt also eine Drehstreckung in der komplexen Zahlenebene
Bei der komplexen Darstellung ist dein B die Zahl z = 3 + 5i.
Zur Drehung um den Winkel φ benötigt man eine Zahl a mit dem Winkel φ und dem Radius 1. Man schreibt dafür
a = eiφ = cos φ + i sin φ
Im Beispiel: Da φ = 90° = π/2 ist: einfach a= i
Die Rotation rechnet man: i*(3+5i) = 3i - 5 . Das entspricht dem gesuchten Punkt B' (-5/3).
In den Spalten von Matrizen stehen die Bildvektoren der beiden Basisvektoren des Koordinatensystems in den Spalten der Matrizen
Für eine Drehung um φ ist das die Rotationsmatrix
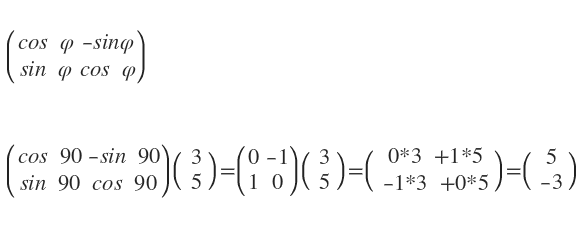
Du bekommst wie gewünscht den Bildpunkt B'(5/-3)
Bei Drehungen um einen andern Punkt verknüpfst du 2 Translationen und eine Drehung: Führe zuerst mit einer Translation (Addition) das Zentrum in den Koordinatenursprung, dann drehst du um das Zentrum. Den Bildpunkt und das Zentrum verschiebst du jetzt wieder so, dass das Zentrum am ursprünglichen Ort liegt.
Wenn du die Koordinaten vor und nach der Drehung und das Drehzentrum kennst, kannst du den Drehwinkel am einfachsten mit dem Skalarprodukt berechnen. Dazu benutzt du die Vektoren