Beweis gleichseitiges Dreieck

Question

Ich hatte bereits schon mal zu diesem Thema gefragt. Die Benamung seht ihr auf meiner Skizze.

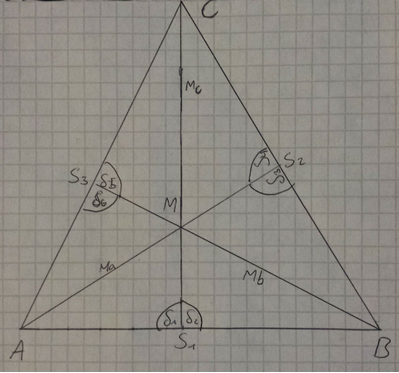
Mein neuer Beweis sieht so aus:

(1) delta_1 kongruent mit delta_2 kongruent mitdelta_3 kongruent mit delta_4 kongruent mitdelta_ 5 kongruent mit delta_6
(2) AS₁ kongruent BS₁BS₂ kongruent CS₂CS₃ kongruent AS₃
(3) MC kongruent MB kongruent MA = r ( Radien des Aussenkreises )MS₁ kongruent MS₂ kongruent MS₃ = r ( Radien des Innenkreises )
(4) Beweis Kongruenz Dreieck AS₁M und Dreieck BS₁M
AS₁ kongruent BS₁delta_1 kongruent delta_2S₁M kongruent S₁MMA kongruent MB
Analog zu Dreieck BS₂M kongruent Dreieck CS₂Mund           Dreieck CS₃M kongruent Dreieck AS₃M
=> Dreieck ABC gleichseitig w.z.b.w

Comments

für meinen Geschmack beinhaltet der Beweis ein bisschen zu oft das Wort kongruent ^^. Was meinst du z.B. mit delta₁ kongruent mit delta₂? Delta1 = Delta2?

Gruß
EmNero

---

Was genau sind die Voraussetzungen für deine Behauptung und welche Linien hast du ins Dreieck gezeichnet?

---

@EmNero:

ja Delta1 = Delta2 ^^.

@Lu

Sry, hatte hier schon mal gefragt und vergessen zu verlinken. Es gilt die Behauptung zu beweisen, dass:

Dreieck ABC gleichseitig ist, wenn der Mittelpunkt von Innen- und Aussenkreis deckungsgleich sind.

Die Linien sind die Mittelsenkrechten bzw. Seitenhalbierenden bzw. Winkelhalbierende ^^.

Gruß, hydra

Answer 1

Es gilt  der Satz von Viviani → s+t+u = 3  *  r   und  3  *  r  =  h  !!

Comments

Der Satz von Viviani setzt ein gleichseitiges Dreieck voraus. Ich soll beweisen, dass es sich um ein gleichseitiges Dreieck handelt.