Funktion, Nullstellen und Extrem- Wendepunkte bestimmen.

Question

Man diskutiere die Funktion definiert durch f(x) = $${ e }^{ -\frac { 1 }{ { x }^{ 2 } } }$$ für x ̸= 0 und f(0) = 0 (d. h. man bestimme Nullstellen, Extremwerte, Wendepunkte, Grenzwerte, Symmetrieeigenschaften, . . . ) und skizziere den Funktionsgraphen. 

Ich komm mit der Funktion nicht klar. Ihrgendwie gibt es ja garkeine Nullstelle außer die oben definierte und Extremstellen gibt es ja ihrgendwie auch nicht ?

Answer 1

f(x) = e^{- 1/x^2} 

f'(x) = 2/x^3·e^{- 1/x^2}

f''(x) = e^{- 1/x^2}·(4/x^6 - 6/x^4)

Symmetrie 

Achsensymmetrie, da x nur in geraden Potenzen auftritt --> f(-x) = f(x)

Grenzwerte an den Grenzen des Definitionsbereichs

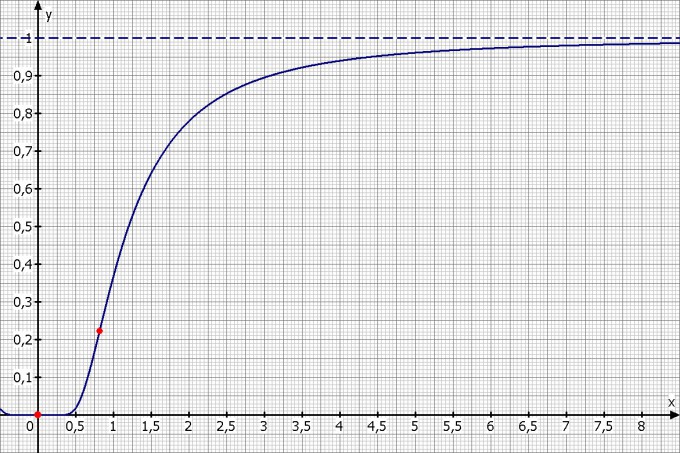
lim (x-->∞) f(x) = e^0 = 1

lim (x-->0+) f(x) = e^{-∞} = 0

Nullstellen f(x) = 0

e^{- 1/x^2} = 0 --> keine (die e-Funktion wird nie 0)

Extrempunkte f'(x) = 0

f(x) ist für alle x ≠ 0 immer größer als Null

f(0) ist 0 und damit ein Tiefpunkt.

Wendepunkte f''(x) = 0

e^{- 1/x^2}·(4/x^6 - 6/x^4) = 0

4/x^6 - 6/x^4 = 0 --> x = ± √6/3 = ± √6/3 = 0.816

f(√6/3) = e^{- 1/(√6/3)^2} = 0.223

Skizze

Comments

ja hab gerade ausgebessert

---

Warum soll es keine Extrempunkte geben? Offensichtlich ist der Ursprung absolutes Minimum der Funktion.

---

Offensichtlich ist die Funktion im Ursprung nicht definiert.

---

Lt. Aufgabenstellung ist \(f(0)=0\).

---

Ok. Danke für den Hinweis. Das hab ich wohl überlesen.