Also, bei a) geht es ja darum, dass er per Zufall noch 12 aus den restlichen 42 Fragen richtig beantwortet.
Das Ganze ist wie ein Bernoulli-Experiment, d.h. es gibt, wenn man sich mal ein Baumdiagramm vorstellt, jedes Mal nur die Unterteilung in jeweils 2 neue Pfade, und die entsprechenden Wahrscheinlichkeiten sind immer gleich: immer nur richtig (1/3) oder falsch (2/3).
Bei "mindestens 20", sprich mindestens 12 von 42, würde ich zunächst mal das Gegenereignis berechnen, also dass er weniger als 12 schafft. Dazu benutzt man die Formel der Bernoulli-Verteilung. Es wird immer jeweils die Anzahl der Pfade, auf die das Ereignis zutrifft, mal die jeweilige Wahrscheinlichkeit hoch die Anzahl, wie oft es zutreffen soll, mal die jeweilige Wahrscheinlichkeit des anderen möglichen Ergebnisses hoch die Anzahl, wie oft dies zutreffen soll, gerechnet. Hört sich (falls man es vorher noch nicht hatte) auf den ersten Blick ein bisschen kompliziert an, ist aber eigentlich ganz logisch.
In dem Fall wäre das dann:
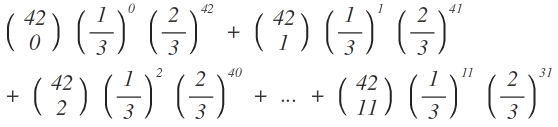
≈ 0,20849
Davon dann das Gegenereignis, also dass er mindestens 12 Fragen von 42 (also insgesamt mindestens 20 von 50) richtig beantwortet: 1 - 0,20849 = 0,79151 = 79,151%.
Bei der b) dann etwa dasselbe Verfahren, nur dass die Formel aufgrund der hohen Anzahl der einzelnen Ereignisse noch länger aussieht. ^^