Finde die Transformationsmatrix nach einer Verschiebung

Question

Aufgabe:Ein Körper wurde im Koordinatensystem verschoben. Was ist passiert? Finde die Transformationsmatrix

Problem/Ansatz:
Moin, ich hab die Objektmatrix eines Körpers (Quaders) A und die des Körpers nach einer Verschiebung B. Jetzt soll ich herausfinden wie der Körper bewegt wurde. Dafür brauche ich ja die Transformationsmatrix, oder Matrizen falls der Körper mehrfach bewegt wurde. Wie muss ich daran gehen?

Text erkannt:

Matrix A:

Matrix B:

Answer 1

Ich weiß zwar nicht, in welchem Raum sich das ganze abspielt, was eine Objektmatrix ist und wo da der Quader ist, aber die Transformation von A nach B ist offensichtlich.

Comments

Die Matrix formt einen Körper im XYZ-Koordinatensystem. Objektmatrix bezeichnet nur das sammeln der gegebenen Punkte bzw. Vektoren in Matrixform. Und "offensichtlich" hilft mir nicht weiter

---

formt einen Körper ... sammeln der Punkte...

hilft auch nicht weiter, wenn Du nicht klar sagst, wo die Punkte in der Matrix konkret(!) stehen und was die Elemente (oder Spalten oder Zeilen) der Matrix konkret(!) bedeuten. xyz-Koordinaten sind nicht erkennbar.

Answer 2

Die Verschiebung eines Punktes \(P\) um einen Vektor \(\vec{v}\) auf den Punkt \(P'\) lässt sich schreiben als

\(\overrightarrow{OP'}=\overrightarrow{OP}+\vec{v}\) und damit \(\vec{v}=\ldots\)

Nun vergleiche die Koordinaten deiner Punkte.

Ich weiß nicht, was genau die Werte in der vierten Zeile bedeuten sollen, aber die Werte in den ersten drei Zeilen stellen wohl die Koordinaten im 3D-Raum dar. Und damit ist der Vektor \(\vec{v}\) direkt berechenbar.

Comments

So kann man spekulieren (war auch meine Idee). Ich sehe es aber erstmal als Aufgabe des FS hier klarzustellen. (In der letzten Zeile fehlt ein \ ).

---

Die letzte Zeile der Matrix ist Teil der Transformationsschreibweise und bedeutet nur, dass jede Spalte ein Punkt ist. Leider wird nach den Transformationsmatrizen gefragt statt einfach nur dem Vektor. Es gibt ja eine Vorlage der Transformationsmatrix für jede mögliche Bewegung.

Der Vektor müsste doch (3;-3;-2) sein

---

bedeutet nur, dass jede Spalte ein Punkt ist.

Vermutlich meinst Du: "jede Spalte über der vierten Zeile".

Häppchenweise erklärst Du weiter, was hier gemeint ist (das gehört ungefragt zur Aufgabenstellung).

Es gibt ja eine Vorlage der Transformationsmatrix für jede mögliche Bewegung.

Auch das erklärst Du uns wieder nicht. Warum muss man da wieder nachfragen? Wie sieht denn diese "Vorlage" aus?

---

Die Aufgabenstellung war sehr allgemein, da der Prof nur meinte sowas in der Art könnte drankommen. Die Zahlenwerte der Matrizen stimmen allerdings zu der Verschiebung eines Quaders im XYZ-Koordinatensystem.

Die Vorlage ist lange Liste von 4x4 Matrizen die meist der Einheitsmatrix ähnlich sehen und manchmal noch Platz für eine oder mehrere Variable des Vektors oder des Drehwinkels haben. Sie werden dann mit der Ausgangsmatrix A multipliziert und führen zu Matrix B. Sowas unter anderem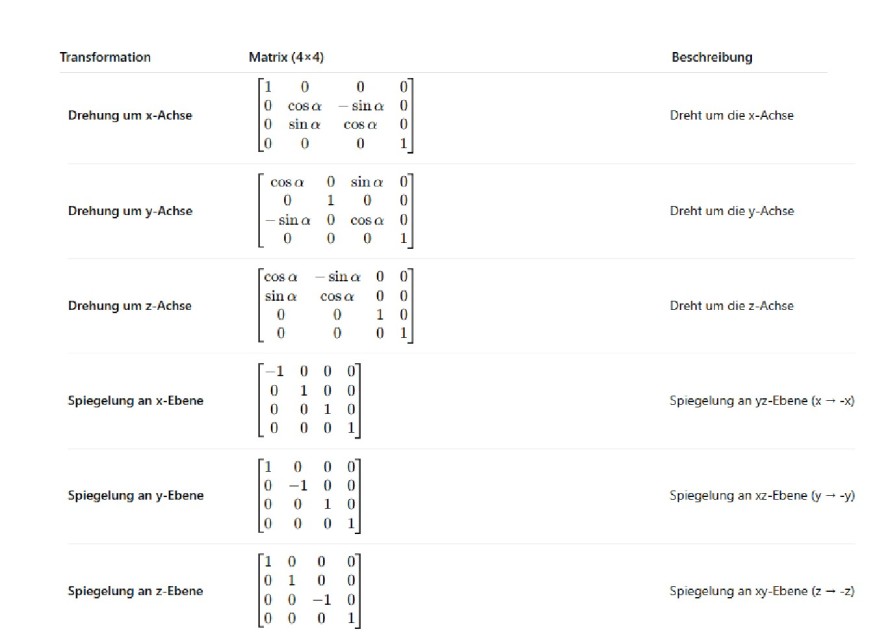

Text erkannt:

\begin{tabular}{|l|l|l|}
\hline Transformation & Matrix ( \( 4 \times 4 \) ) & Beschreibung \\
\hline Drehung um x-Achse & \( \left[\begin{array}{cccc}1 & 0 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1\end{array}\right] \) & Dreht um die x-Achse \\
\hline Drehung um y-Achse & \( \left[\begin{array}{cccc}\cos \alpha & 0 & \sin \alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \alpha & 0 & \cos \alpha & 0 \\ 0 & 0 & 0 & 1\end{array}\right] \) & Dreht um die y-Achse \\
\hline Drehung um z-Achse & \( \left[\begin{array}{cccc}\cos \alpha & -\sin \alpha & 0 & 0 \\ \sin \alpha & \cos \alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\right] \) & Dreht um die z-Achse \\
\hline Spiegelung an x -Ebene & \( \left[\begin{array}{cccc}-1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\right] \) & Spiegelung an yz-Ebene ( \( \mathrm{x} \rightarrow-\mathrm{x} \) ) \\
\hline Spiegelung an y -Ebene & \( \left[\begin{array}{cccc}1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\right] \) & Spiegelung an xz-Ebene ( \( y \rightarrow-y \) ) \\
\hline Spiegelung an z-Ebene & \( \left[\begin{array}{cccc}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1\end{array}\right] \) & Spiegelung an xy-Ebene ( \( z \rightarrow-z \) ) \\
\hline
\end{tabular}