Funktionenschar fa(x)=0,25(x^4-ax^2). a soll so gewählt werden, dass der Graph bei x=1 einen Wendepunkt hat.

Question

der parameter der funktionenschar fa(x)=0,25(x^4-ax^2) soll so gewählt werden, dass der graph bei x=1 einen wendepunkt hat. wie lauten dann die koordinanten des zweiten wendepunktes?

wo liegen die wendepunkte von fa? stellen sie die gleichung der wendetangenten von f1 auf.

Answer 1

Was ist denn die Bedingung für einen Wendepunkt an der Stelle x = 1 ?

Answer 2

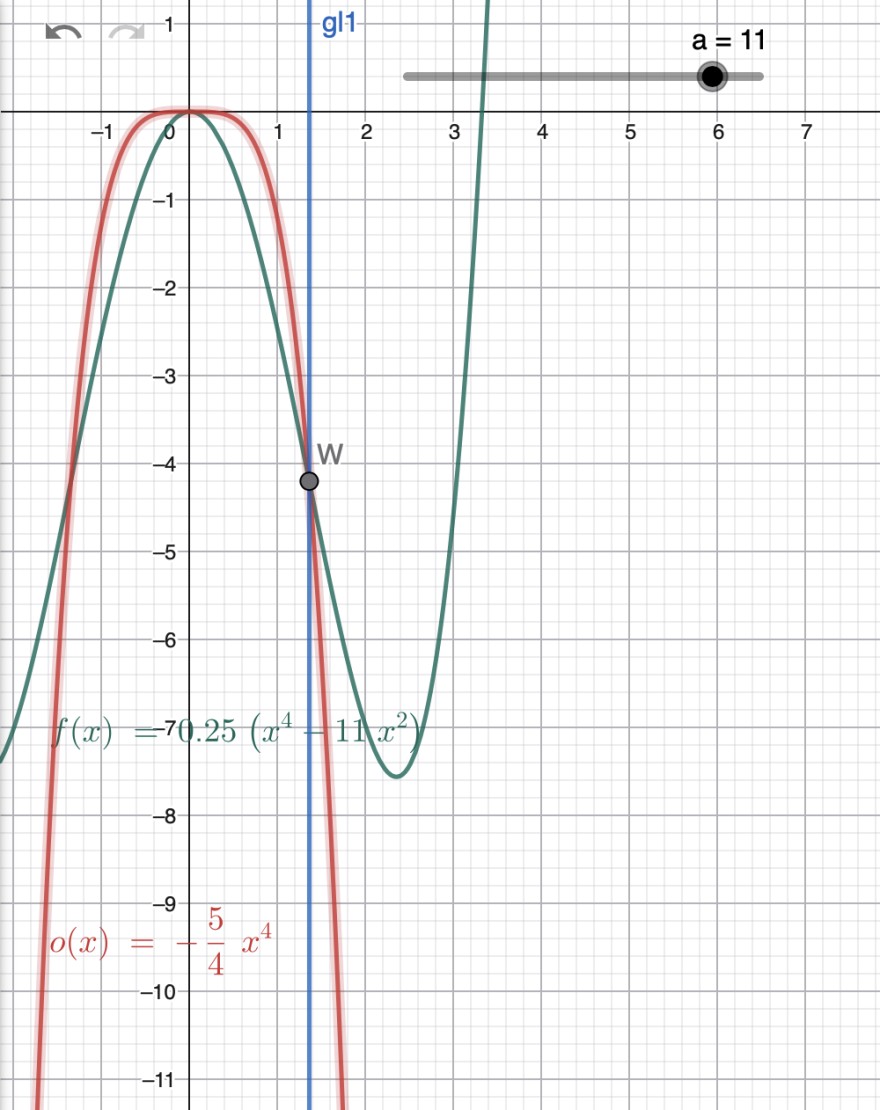
Der Parameter der Funktionenschar \( f_a(x)=0,25(x^4-ax^2) \) soll so gewählt werden, dass der Graph bei x=1 einen Wendepunkt hat.
1.)Wie lauten dann die Koordinaten des zweiten Wendepunktes?

\( f'_a(x)=0,25(4x^3-2ax) \)

\( f''_a(x)=0,25(12x^2-2a) \)

\( 0,25(12x^2-2a)=0 \)   →  \( x^2= \frac{a}{6}\)   → \( x_1= \sqrt{\frac{a}{6}} \)  →   \( x_2= -\sqrt{\frac{a}{6}} \)

...bei x=1 einen Wendepunkt hat.

\( 1= \sqrt{\frac{a}{6}} \)   → \( a=6\)   →   \( f_6(x)=0,25(x^4-6x^2) \)

\( f_6(1)=0,25(1-6) =-1,25\)    W_1 \( (1|-1,25)\)

\( f_6(-1)=0,25(1-6) =-1,25\)   W_2 \( (-1|-1,25)\)

\( a>0\)