Approximation Aufgabe trotz lösung nicht verstanden

Question

Verstehe überhaupt nicht was mein Ansatz wäre bei dieser Aufgabe selbst die Lösung hilft mir nicht 

Das ist die dazugehörige Lösung

Comments

Die "Lösung" besagt:

Du sollst erst das angegebene Integral ausrechnen.

Dazu erst mal die Klammer im Integranden auflösen.

Dann das Resultat der Integration mit den Variablen a_0 und a_1 minimieren.

Es sollte für die Minimalstelle a_0= -4/35 und a_1 = 36/35 rauskommen.

---

Danke für die schnelle Antwort. Ich wüsste jedoch nicht wie man von der Aufgabenstellung auf das gegebene Integral  kommt.  Ein Rechenweg wäre sicherlich hilfreich zu dieser Aufgabe.

---

 Ich wüsste jedoch nicht wie man von der Aufgabenstellung auf das gegebene Integral  kommt.  

Lineare Funktion heisst, du suchst

g(x) = mx + q  (Gesucht m und q)

oder eben mit andern Variabelnbezeichnungen g(x) = a0 + a1*x gesucht a0 und a1.

Nun die Differenz der beiden Funktionen ausrechnen. An jeder Stelle quadrieren und in den Integranden schreiben.

Q = ∫_(0)^1 ( x^{3/2} - (mx+q))^2 dx

Klammern auslösen und Integral ausrechnen, schaffst du doch selbst.

---

erst das angegebene Integral ausrechnen

Das ist doch wohl hoffentlich nur symbolisch gemeint.

---

hj2177: Wie würdest du denn die Integration und das Minimieren nachher ganz genau abkürzen?

---

Man kann sich einen ganzen Haufen Arbeit sparen, wenn man deine Reihenfolge "Erst integrieren - dann differenzieren" umkehrt.

---

Und wonach leitest du genau ab? Partiell nach a0 und a1?

---

Wonach denn sonst ?

d/da ₀∫¹ (f(x) - φ(x))² dx = ₀∫¹ d/da (f(x) - φ(x))² dx = 2·₀∫¹ (f(x) - φ(x))·dφ/da dx

wobei a nacheinander für a₀ und a₁ steht.

Answer 1

@ hi5399
Verstehe überhaupt nicht was mein Ansatz wäre bei dieser Aufgabe
selbst die Lösung hilft mir nicht

Du hast eine Funktion
f ( x ) = x^{3/2}
Du sollst im Intervall zwischen 0..1  eine " Ausgleichsgerade "  dafür finden.
Das Ergebnis vorwegnehmend
g ( x ) = m * x + b
g ( x ) = 36/35 * x - 4/35

~plot~ x^{3/2} ;  36/35 * x - 4/35 ; [[ 0 | 1 | -0.1 | 1 ]] ~plot~

Die Differenz an einer Stelle wäre
f ( x ) - g ( x )
Es wird das Quadrat genommen
[ f ( x ) - g ( x )  ]^2
Aufsummiert  zwischen 0 und 1
∫ [ f ( x ) - g ( x )  ]^2 zwischen 0 und 1
∫ [ x^{3/2} - m * x + b  ]^2 zwischen 0 und 1



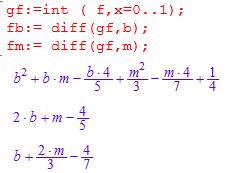
Davon wird partiell abgeleitet nach b und m
Zur Berechnung des Extrempunkts werden die beiden letzten
Terme zu null gesetzt und dann b und m berechnet.
b und m ergeben sich wie in deiner Lösung angegeben.

mfg Georg