Bestimme über welchem Körper f diagonalisierbar ist

Question

Sei \(f:M_2(\mathbb{K})\rightarrow M_2(\mathbb{K})\) definiert durch

  .

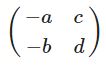Bestimme ob f diagonalisierbar ist für jeden Körper \(\mathbb{K}\in\) { \( \mathbb{C},\mathbb{R}\),\(\frac { \mathbb{Z} }{ 2\mathbb{Z} }\)}.

Zuerst stimmt die Äquivalenz f diagonalisierbar genau dann wenn A diagonalisierbar?

Ich habe mal das charakteristische Polynom ausgerechnet und bekam:

\(\lambda^2+(a-d)\lambda+(cb-ad)\)

und das muss ich ja jetzt Null setzen und schauen, was für Eigenwerte rauskommen, bzw. über welchem Körper sie definiert sind und dann mit anderen Argumenten zeigen, ob A diagonalisierbar ist. Bin ich so auf dem richtigen Weg?

Kann mir jemand helfen, die Eigenwerte zu bestimmen?

Comments

Ist in der vollständigen Fragestellung irgendwie ersichtlich, weshalb da -a und -b steht? 

Sollen z.B. a und b positiv sein? 

Wenn nicht, kannst du wohl genau so gut mit u,v,w,x arbeiten und die beiden Minus weglassen. Zum Schluss kann man ja immer noch wieder auf die gegebenen Parameter umschreiben. 

---

Möglicherweise soll \(f\) die Matrix \(\begin{pmatrix}a&c\\b&d\end{pmatrix}\) auf die Matrix \(\begin{pmatrix}-a&c\\-b&d\end{pmatrix}\) abbilden?

---

Eigentliche Fragestellung offenbar hier: https://www.mathelounge.de/373631/funktion-f-diagonalisierbar-bei-ve… 

Answer 1

> stimmt die Äquivalenz f diagonalisierbar genau dann wenn A diagonalisierbar?

Was ist A?

> Bin ich so auf dem richtigen Weg?

Ja

> Kann mir jemand helfen, die Eigenwerte zu bestimmen?

Verwende die pq-Formel. Dann bekommst du

        λ = -(a-d)/2 + 1/2 √(d²+2ad-4bc+a²) oder

        λ = -(a-d)/2 - 1/2 √(d²+2ad-4bc+a²).