Rekonstruktion von Funktionen dritten grades Steckbriefaufgabe

Question

Aufgabe: gesucht ist eine ganz rationale Funktion dritten Grades mit dem Tiefpunkt P(1|-2), deren Wendepunkt im Koordinatenursprung liegt.

Hab meinen Ansatz im Bild.

Brauche Hilfe da ich nicht weiter komme und es gerne verstehen würde :/

Answer 1

Du  gehst nach
http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm

und gibst im Feld
" Eigenschaften eingeben "

f ( 1 ) = -2
f ' ( 1 ) = 0
f ( 0 ) = 0
f '' ( 0 ) = 0

ein ( Die 4 obigen Zeilen kopieren und dort einfügen )

und drückst die Schaltfläche " berechnen ".
Dann wird dir die Funktion berechnet.

f(x) = x^3 - 3·x

Bei den Ableitungen mußt du das Zeichen "  '  "
auf der Taste rechts neben dem " Ä " verwenden. " f ' "

Falls dir an einer manuellen Berechnung
gelegen ist dann wieder melden.

Comments

Das klappt leider nicht bei mir trotzdem danke

---

Sollte aber.

f ( 1 ) = -2
f ' ( 1 ) = 0
f ( 0 ) = 0
f '' ( 0 ) = 0

f ( x ) = a * x^3 + b * x^2 + c * x + d
f ( 0 ) = 0   = > d = 0

f ( x ) = a * x^3 + b * x^2 + c * x
f ´( x ) = 3 * a * x^2 + 2 * b * x + c
f ´´( x ) = 6 * a * x + 2 * b
f '' ( 0 ) = 6 * a * 0 + 2 * b = 0  => b = 0

f ( x ) = a * x^3 + c * x
f ´( x ) = 3 * a * x^2 + c
f ( 1) = a * 1^3 + c * 1 = -2
f ´( 1 ) = 3 * a * 1^2 + c  = 0

a  + c  = -2
3 * a   + c  = 0

c = -2 - a
3 * a   + ( -2 - a )  = 0
2a - 2 = 0
a = 1
c = -2 - 1
c = -3

f(x) = a * x³ + c·x
f(x) = x³   - 3·x

Answer 2

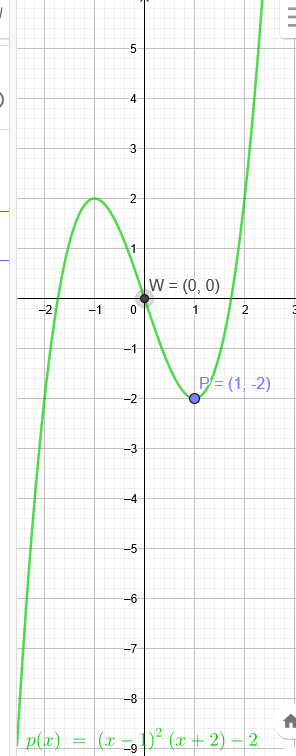
 "Gesucht ist eine ganz rationale Funktion dritten Grades mit dem Tiefpunkt P(1|-2), deren Wendepunkt im Koordinatenursprung liegt."

Parabeln 3.Grades sind punktsymmetrisch im Wendepunkt

Tiefpunkt P(1|-2)→Hochpunkt Q(-1|2)

Ich verschiebe um 2 Einheiten nach oben:

Tiefpunkt P´(1|0)→Hochpunkt (-1|4),   W´(0|2)  und Q´(-1|4)

\(f(x)=a*(x-1)^2*(x-N)\)

W´(0|2)

\(f(0)=a*(0-1)^2*(0-N)→-a*N=2→     a=- \frac{2}{N} \)

\(f(x)=- \frac{2}{N} *(x-1)^2*(x-N)\)

Q´(-1|4)

\(f(-1)=- \frac{2}{N} *(-1-1)^2*(-1-N) \)

\(- \frac{2}{N} *(-1-1)^2*(-1-N)=4 \)        \(N=-2 \)       \(a=1 \)

\(f(x)=(x-1)^2*(x+2)\)

\(p(x)=(x-1)^2*(x+2)-2\)