Vorwort:
Die ersten Pyramiden stammen aus einer Zeit, die wir uns kaum vorstellen können. Die erste registrierte Pyramide ist die Djoser-Pyramide, die während der 3. Dynastie des Alten Reiches um 2560 v. Chr. gebaut wurde. Diese ist jedoch eine Stufenpyramide mit einer nichtquadratischen Fläche.
Es gibt jedoch Pyramiden, wie die Cheops-Pyramide, welche man ganz einfach anhand der Formeln für eine quadratische Pyramide berechnen kann. Das heißt aber nicht, dass die Djoser-Pyramide nicht berechnet werden kann, sondern vielmehr, dass die Angelegenheit dort schwieriger wird.
Ich werde nun anhand eines realen Beispiels (Cheops-Pyramide) den Vorgang bei der Berechnung einer Quadratischen Pyramide erläutern.
Begriffserklärungen und Aufbau:
Das ist die Cheops-Pyramide:

Da wir heute sehr wissensbegierig sind, wollen wir alles über die Maße der Pyramide wissen! Doch vorab müssen wir erst einmal wissen was man überhaupt an einer solchen Pyramide ausrechnen kann. Viele Dinge lassen sich mit dem Satz des Pythagoras ausrechnen, da sich zwei rechtwinklige Dreiecke bilden. Siehe hier:
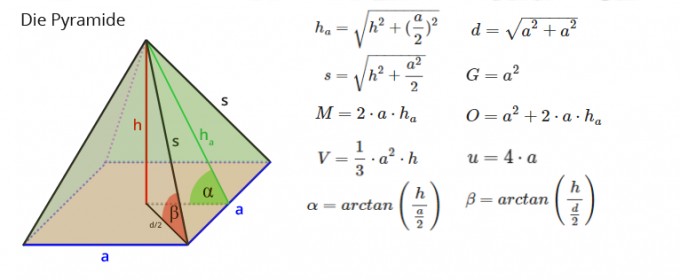
Es gibt also das Volumen(V), die Mantelfläche(M), die Oberfläche(O), die Diagonale(d), Seitenlänge(a), Seitenkante(s), die Höhe auf der Seitenlänge(ha),die Höhe(h) und den Umfang(u).
Für diejenigen, die nicht wissen was eine Mantelfläche(M) oder Oberfläche(O) ist hier eine kleine Grafik zur Veranschaulichung:

Die Mantefläche (M) ist der grün-markierte Teil der auseinandergeklappten Pyramide, wobei die grün-markierte Oberfläche(O) und die blau-markierte Grundfläche(G) addiert werden.
Da wir nun die Formeln kennen brauchen wir noch Werte, um die Cheops-Pyramide zu berechnen. Laut Wikipedia ist die Cheops-Pyramide heutzutage 138.75m hoch und verfügt außerdem über eine Höhe von der Seite(a) von 186.02m (siehe Grafik oben).
Unsere Aufgabe ist es nun alle möglichen Werte der Cheops-Pyramide zu bestimmen.
Anwendungsbeispiel:
Für unser Anwendungsbeispiel sind uns von der Cheops-Pyramide folgende Werte bekannt:
$$ h=138.75m\quad {h}_{a}=186.02m $$ Zu Beginn möchte ich wissen wie lang die Seite (a) also das Basismaß der Cheops-Pyramide ist. Ein kurzer Blick in unsere Formelsammlung verrät uns, dass es am besten ist diese Formel zu verwenden, da wir bei dieser genügend Variablen kennen, um die zu gesuchte Seite zu bestimmen:$$ {h}_{a}=\sqrt{h^2+\left(\frac{a}{2}\right)^2} $$ Nun kommt ein sehr essenzieller Teil der Körperberechnung. Es ist unglaublich wichtig zu verstehen wie man eine Formel umstellt. Man kann bei dieser Formel die Wurzel ganz einfach auflösen in dem man beide Seiten quadriert:$$ {h}_{a}^2=h^2+\left(\frac{a}{2}\right)^2 \quad | -h^2$$ Nun müssen wir nur das "a" alleine auf eine Seite bringen: Dies tun wir, in dem wir die Höhe mit der Subtraktion auf die andere Seite bringen:$$ {h}_{a}^2-h^2=\left(\frac{a}{2}\right)^2 \quad |\left(\frac{a}{2}\right)^2 ⟹ \frac{a^2}{4}$$ So weit so gut, jedoch haben wir noch nicht das gewünschte "a" sondern (a/2)^2. Wir müssen nun also die Klammern auflösen; daraus ergibt sich:$${h}_{a}^2-h^2=\frac{a^2}{4} \quad | \cdot 4 \quad | \sqrt{} $$ Nun müssen wir noch die 4 auf die andere Seite bringen und die Wurzel ziehen, sodass wir "a" erhalten:$$a=\sqrt{(ha^2-h^2) \cdot 4}$$ Setzen wir dort also unsere Werte ein erhalten wir für "a":$$a=\sqrt{(186.02^2-138.75^2) \cdot 4}\approx 247.81m$$ Meist brauch man nur einmal die Formeln umstellen, um den Rest der Pyramide zu berechnen. Wir müssen jetzt nur noch die bekannten Maße in die Formeln einsetzen, um alle Werte zu kalkulieren:$$s=\sqrt{138.75^2+\frac{247.81^2}{2}}\approx 223.51m$$$$O=247.81^2+2\cdot 247.81 \cdot 186.02 \approx 153605.03m^2$$$$V=\frac{1}{3}\cdot 247.81^2 \cdot 138.75 \approx 2840203.07m^3$$$$M=2\cdot 247.81 \cdot 186.02 \approx 92195.23m^2$$$$ u=4 \cdot 274.81 \approx 1099.24m $$ Nun kann man noch bestimmen in welchem Winkel die Pyramide sich in den Himmel neigt, bei der Cheops-Pyramide geht das wie folgt:$$α=\arctan\left( \frac{{138.75}_{}}{\frac{247.81}{2}} \right)\approx48.24°$$ Den letzten Wert, den wir jetzt noch ausrechnen werden, ist die Neigung der Seitenkante:$$α=\arctan\left( \frac{{138.75}_{}}{\frac{\sqrt{247.81^2+247.81^2}}{2}} \right)\approx38.37°$$
Nun sind wir fertig und wissen die Näherungsmaße der Cheops-Pyramide und können uns zurücklehnen.
Es werden in dieser Artikelreihe noch folgende Körper aufgeführt:
Die Kugel, der Zylinder und der Kegel.
Ich hoffe, dass euch mein Artikel gefällt.