Vektorenrechnung Oktaeder im würfel

Question

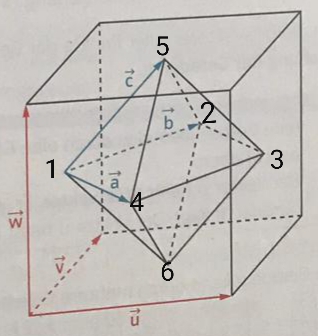
Aufgabe:
A)
Die Richtungvektoren a,b,c bestimmen als Linearkombination der Vektoren u,v,w
B)

Mögliche Eckpunkte  des Oktaeders bestimmen. Kantenlänge des würfels jeweils 6

C)

Volumen  des Oktaeders bestimmen

Ansatz:

A) a=0.5u-0.5v, b=0.5v+0.5u, c=0.5w+0.5u

B) allg=(u,v,w)

1=(0/3/3), 2=(3/6/3), 3=(6/3/3), 4=(3/0/3), 5=(3,3,6), 6=(3/3/0)

Ist das richtig?

C) hier habe ich keinen Ansatz

Answer 1

Aloha :)

(a) ist korrekt. (b) ist korrekt, wenn die Koordinatenachsen auf \(\vec u, \vec v, \vec w\) liegen.

In (c) ist der Betrag des Kreuzproduktes \(\vec a\times\vec b\) gleich der Fläche \(1234\). Skalare Multiplikation dieses Kreuzproduktes mit \(\vec c\) wirkt so, als würdest du mit der Höhe multiplizieren (weil der von \(\vec c\) senkrechte Anteil zu \(\vec a\times\vec b\) bei der Multiplikation verschwindet). Das Volumen einer Pyramide ist 1/3 Grundfläche mal Höhe, also musst du den Betrag des Skalarproduktes noch durch 3 teilen. Dieses Volumen hast du oberhalb und unterhalb der Fläche \(1234\). Also lautet die Formel für das gesuchte Volumen:$$V=\frac{2}{3}\left|\left(\vec a\times\vec b\right)\cdot\vec c\right|$$