Betragsungleichung mit zwei Beträgen: x−|2x+4|>1−|x−2|

Question

Aufgabe:

x−|2x+4|>1−|x−2|

Problem/Ansatz:

mein Ansatz wäre | (..)² ... wie muss ich hier den Fall unterschieden?

Bsp. 1 Fall positiv = 2x+4>0?

Danke

Answer 1

Also wenn da stehen soll:

$$x-|2x+4|>1-|x-2|$$

Dann gibt es folgende Fälle zu beachten:

Fall 1:

$$x \geq -2 \land x < 2$$
$$x-|2x+4|>1-|x-2|$$
$$x-(2x+4)>1-(-(x-2))$$
$$x < -3/2$$

Lösung: [-2;-3/2)

-------------------------------------------------------------------

Fall 2:

$$x < -2 \land x < 2$$
$$x-|2x+4|>1-|x-2|$$
$$x-(-(2x+4))>1-(-(x-2))$$
$$x > -5/2$$

Lösung: (-5/2; -2)

-------------------------------------------------------------------

Zusammen also:

Lösungsintervall: $$(-5/2; -3/2)$$

-------------------------------------------------------------------

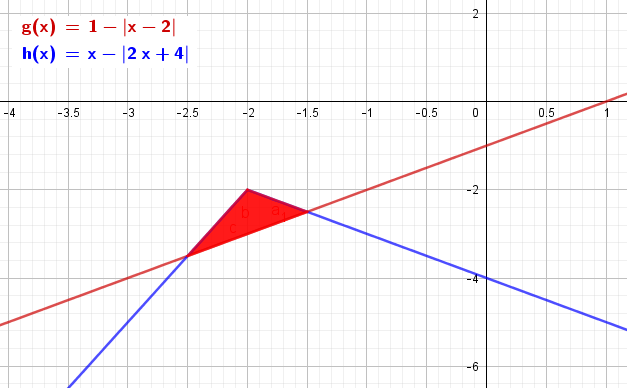
Grafik: