Satz von Bayes - Teilmengenfrage

Question

Hey!

Kann mir jemand sagen, wieso man in b) einfach P(A) schreiben kann? Als Erklärung steht da zwar Teilmenge, aber ich verstehe den Sinn dahinter nicht.

Vielleicht kann mir jemand kurz erläutern, wieso ich so "einfach" diesen Teil mit P(A) ersetzen kann.

Ich ersetze damit praktisch diesen oberen Ausdruck: P(A|Fc)⋅P(Fc)

Fragenstellung:

Nach dem Picknick vermisst Familie Schmidt ihren Hund. Es gibt drei Moglichkeiten, wo der Hund gefunden werden
kann:
A: Er ist nach Hause gelaufen und erwartet die Familie freudig vor der Haustur. ¨
B: Er bearbeitet noch den großen Knochen auf dem Picknick-Platz und ist noch immer dort.
C: Er streunt im Wald.
Aufgrund der Gewohnheiten des Hundes kennt man die Wahrscheinlichkeiten fur das Eintreten der Ereignisse A, B ¨
und C:
P(A) = 0.25
P(B) = 0.5
P(C) = 0.25

Familie Schmidt schickt eines ihrer Kinder zum Picknick-Platz zuruck und ein anderes Kind an den Waldrand. Wenn ¨
der Hund noch am Picknick-Platz ist, findet man ihn mit 90 %-iger Wahrscheinlichkeit. Streunt er aber im Wald, so
betragt die Wahrscheinlichkeit nur noch 50 %.
(a) Mit welcher Wahrscheinlichkeit wird eines der Kinder den Hund finden?
(b) Wie groß ist die (bedingte) Wahrscheinlichkeit dafur, dass Familie Schmidt ihren Hund bei der Ruckkehr vor 
der Haustur anzutreffen, falls die Kinder den Hund nicht finden.

Zu b)

Gesucht : \( P\left(A | F^{c}\right)=\frac{P\left(A \cap F^{c}\right)}{P\left(F^{c}\right)}=\frac{P\left(A | F^{c}\right) \cdot P\left(F^{c}\right)}{P\left(F^{c}\right)} \)
\( P\left(F^{c}\right)=1-P(F)=1-0.575=0.425 \)
\( A \cap F^{c}= \) Hund ist zuhaise u. Wind findet inh \( n \).
\( A \cap F^{c}=A \quad\left(d a A \subseteq F^{c}\right) \)
\( \rightarrow P\left(A | F^{i}\right)=\frac{P(A)}{1-P(F)}=\frac{0.25}{0.425}=\frac{10}{17} \)

Answer 1

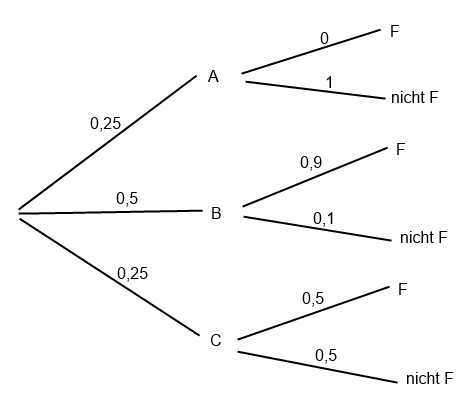
a) P(F) = P(B∩F) + P(C∩F) = P(B)*P(FIB) + P(C)*P(FIC) = 0,5*0,9+0,25*0,5 = 0,575

b) Bayes: P(AIB) = \( \frac{P(A∩B)}{P(A∩B+P(A^{c}∩B)} \) = \( \frac{P(AIB)*P(B)}{...} \)

also:

P(AI\(F^{c} \) ) =   \( \frac{P(A∩F^{c})} {P(A ∩F^{c})+P(A^{c}∩F^{c})} \) = \( \frac{P(A)} {P(A )+P(A^{c}∩F^{c})} \)

laut Baumdiagramm: "der Hund ist zuhause und die Kinder finden ihn nicht", heißt doch "der Hund ist zuhause",

weil die Kinder ihn nicht finden können, wenn er zuhause ist.

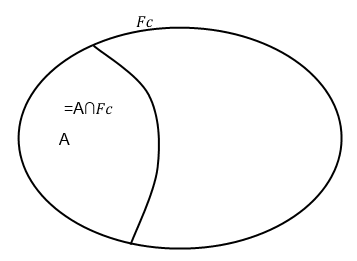
A=(A∩F) ∪ (A∩\(F^{c} \) ) = { }∪ (A∩\(F^{c} \) ) = A∩\(F^{c} \)

Durch den Schnitt mit \(F^{c} \)  wird nichts von A weggenommen, also A⊆\(F^{c} \)

Rechnung weiter =  \( \frac{P(A)} {P(A )+P(B∩F^{c})+P(C∩F^{c})} \) =\( \frac{0,25} {0,25+0,5*0,1+0,25*0,5} \) =10/17

Comments

So okay oder gibt es noch Fragen?