Berechnen Sie anschließend das Mehrfachintegral.

Question

Aufgabe:

Betrachten Sie die Menge B = ((x,y,z) ∈ ℝ³ : x² + y² - 1 ≤ z ≤ 3 ).

Stellen Sie Vol(B) als Mehrfachintegral in Zylinderkoordinaten dar.

Berechnen Sie anschließend das Vol(B).

Answer 1

Skizze:

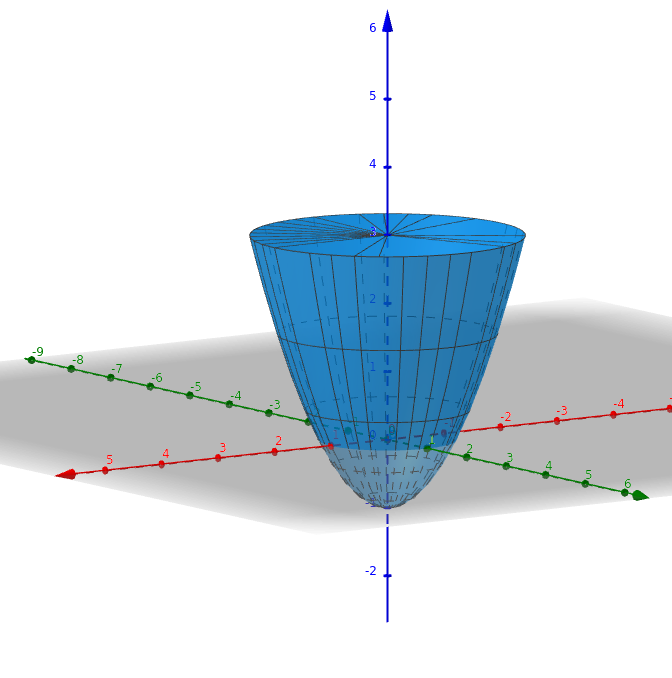
Das Volumen berechnet man mit dem Integral:
$$\iiint_B 1 ~\textrm{d}\mathbf{x}$$

Koordinatentransformation ergibt:

$$\iiint_B r ~\textrm{d}r ~\textrm{d}\varphi ~\textrm{d}z$$

(Die Jacobideterminante der Transformation von kartesischen auf zylindrische Koordinaten ist $r$)

Die Grenze der einzelnen Zylinderkoordinaten sind:

$$r^2 -1 \le z \implies r^2 \le z + 1 \implies r \le \sqrt{z+1}$$

$$z \in [-1,3], \varphi \in [0,2\pi]$$

Also

$$\begin{aligned} \iiint_B r ~\textrm{d}r ~\textrm{d}\varphi ~\textrm{d}z &= \int_{-1}^{3} \int_{0}^{2\pi} \int_{0}^{\sqrt{z+1}} r ~\textrm{d}r ~\textrm{d}\varphi ~\textrm{d}z \\ &= \int_{-1}^{3} \int_{0}^{2\pi} \left[ \frac{1}{2}r^2 \right]_0^{\sqrt{z+1}} ~\textrm{d}\varphi ~\textrm{d}z \\ &= \int_{-1}^{3} \int_{0}^{2\pi} \frac{1}{2}(z+1) ~\textrm{d}\varphi ~\textrm{d}z \\ &= \pi \int_{-1}^{3} (z+1) ~\textrm{d}z \\ &= \pi \left[\frac{1}{2}z^2 +z\right]_{-1}^{3} \\&=8\pi \end{aligned}$$

Comments

Okay vielen Dank das habe ich jetzt verstanden :)

Answer 2

Hallo

da das ein Zylinder ist nimmst du am besten Zylinderkoordinaten, wie es da ja auch steht

Grenzen:  r von 0 bis 1+z, phi von 0 bis 2pi, z oder h von -1 bis 3

Oder was genau ist deine Frage?

lul

Comments

Genau zuerst sollten die Integralgrenzen bestimmt werden also nach meinen Lösungen wäre das r von 0 bis 2, pi von 0 bis 2pi und z von r²-1bis 3. Das habe ich auch noch halbwegs verstanden wie ich darauf kommen.

Dann wird das integral von r mit den oben genanten Grenzen berechnet um das Volumen zu bestimmen:  ∫∫∫ r dzdydx . Da wäre meine Frage wie ich darauf komme wovon ich das Integral nehme, also in diesem Fall r. Wo kommt das her ?

Und dann soll man dieses Mehrfachintegral eben berechnen.

Aber danke schonmal für die erste Antwort ;)