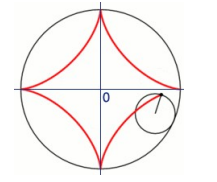
Die Astroide ist diejenige Kurve, die ein Punkt auf einem Kreis mit Radius 1/4 d beschreibt, der innen auf einen Kreis mit Radius d abrollt. Sie wird beschrieben durch die implizite Gleichung
|x|2/3 + |y|2/3 = d2/3 , d∈ R.
Die Parameterdaratellung der Astroide lautet:
\( \vec{a} \) (t) = \( \begin{pmatrix} d cos³t \\ d sin³t \end{pmatrix} \) mit 0 ≤ t ≤ 2π
Berechnen Sie die Bogenlänge der Astroide
(Hinweis: Umgehen Sie das Problem der Fallunterscheidungen beim Wurzel uiehne, indem Sie die Symmtertrie nutzen; integrieren Sie nur über den ersten Quadranten, in dem Sinus und Cosinus positiv sin, und multipilzieren Sie das Ergebnis mit 4.)