Hallo,
das ist doch ein klassisches Problem für den Lagrange-Multiplikator. Bevor es los geht, kann man sich schon ein Bild machen, von dem, was man da berechnet.
Der zweite Teil von \(K\) ist die Einheitskugel im Ursprung, bzw. deren Oberfläche. Der erste Teil ist eine Ursprungsebene mit Normalenvektor \(\begin{pmatrix}1&1&1\end{pmatrix}\). Bringt man beides zum Schnitt, so bildet sich ein Ring im Raum, deren Mittelpunkt im Ursprung liegt. Wie auf diesem Bild zu sehen ist.
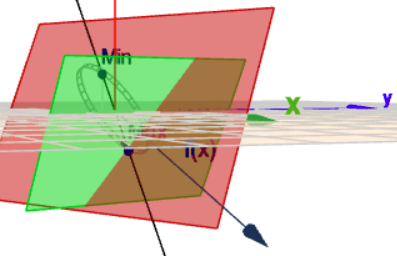
(klick auf das Bild und rotiere die Szene mit der Maus, dann siehst Du es besser)
Die Funktion \(f\) ist linear. D.h. das jedes Niveau von \(f\) eine Ebene im Raum ist. Die grüne Ebene im Bild oben steht für das Niveau \(f=4\) und der Vektor zeigt in die Richtung, in die \(f\) wächst. D.h. das gesuchte Maximum von \(f\) ist in etwa dort, wo die grüne Ebene den Ring berührt. Das Minimum wäre dann genau auf der anderen Seite.
Mit Lagrange geht das so. Zunächst die Lagrange-Funktion aufstellen. Da wir zwei Nebenbedingungen haben, brauchen wir auch zwei Variablen \(\lambda_{1,2}\)$$L(\vec x,\lambda_{1,2}) = 4x_1 + x_2 - 2x_3 + \lambda_1(x_1 + x_2 + x_3) + \lambda_2(x^2_1 + x^2_2 + x^2_3 - 1)$$dann nach den drei Variablen \(x_{1,2,3}\) ableiten und die Ableitung zu 0 setzen$$\frac{\partial L}{\partial x_1} = 4 + \lambda_1 + 2\lambda_2x_1 = 0 \\ \frac{\partial L}{\partial x_2} = 1 + \lambda_1 + 2\lambda_2x_2= 0 \\ \frac{\partial L}{\partial x_3} = -2 + \lambda_1 + 2\lambda_2x_3= 0$$macht drei Gleichungen, bei denen man die \(\lambda\)'s entfernen sollte, Ich ziehe dazu die dritte von den beiden anderen ab$$6 + 2\lambda_2(x_1-x_3) = 0 \\ 3 + 2\lambda_2(x_2 - x_3) = 0$$bleiben noch zwei Gleichungen mit \(\lambda_2\). Die fasse ich zusammen$$\begin{aligned} \implies 6(x_2 - x_3) &= 3(x_1-x_3) \\ 2x_2 - 2x_3 &= x_1 - x_3 \\ 0&= x_1 - 2x_2 + x_3 \\ \end{aligned}$$Macht wieder eine Ebene im Raum, die ich oben im Bild rot dargestellt habe. Alle potentiellen Extremstellen müssen in dieser Ebene liegen. Bringe ich diese mit der Ebene aus \(K\) zum Schnitt, so kommt man zu der schwarzen Geraden. $$g: \quad \vec x = \begin{pmatrix}1\\ 0\\ -1\end{pmatrix} t$$Und der Schnitt mit dem zweiten Teil von \(K\), der Oberfläche der Einheitskugel, liefert dann die beiden Extremstellen$$\vec x_{\max} = \frac 12 \sqrt 2\begin{pmatrix}1\\ 0\\ -1\end{pmatrix}, \quad f(\vec x_{\max}) = 3\sqrt 2 \approx 4,2\\ \vec x_{\min} = \frac12\sqrt 2\begin{pmatrix}-1\\ 0\\ 1\end{pmatrix}, \quad f(\vec x_{\min}) = -3\sqrt 2 $$Falls Du noch Fragen hast, so melde Dich bitte.
Gruß Werner
PS.: die Vermutung von Böllewege war richtig (s. Kommentar unter der Frage)