Question

Eine Etappe der Tour de France führte durch die französischen Alpen.

Hier mussten die Radfahrer große Höhenunterschiede bewältigen.

a) Wie groß war auf der Strecke von La Madeliene nach Aigueblanche das durchschnittliche Gefälle?

b) Wie groß war die durchschnittliche Steigung von Aigueblanche nach Courchevel?

Answer 1

 

wir können mit rechtwinkligen Dreiecken arbeiten;

Strecke La Madeleine - Aigueblanche:

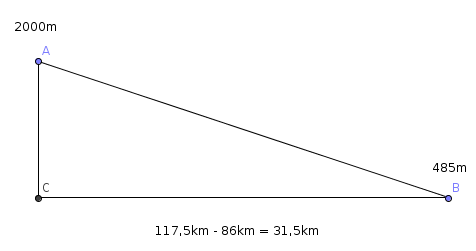
Der Höhenunterschied beträgt 485m - 2000m = -1515m

Minuszeichen, weil es sich um ein Gefälle handelt.

Die waagrechte Entfernung beträgt 31,5km = 31.500m

-1515/31.500 ≈ -0,048095

Das durchschnittliche Gefälle war also ca. 4,8°

 

Strecke Aigueblanche - Courchevel

Analog, diesmal ist es aber eine Steigung

Höhenunterschied: 2004m - 485m = 1519m

Waagrechte Entfernung: 148km - 117,5km = 30,5km = 30.500m

1519/30.500 ≈ 0,0498

Die durchschnittliche Steigung war also ca. 5%

 

Besten Gruß

Comments

warum 485m-2000m?

warum nicht 2000m-485m?

---

Weil man "Ziel minus Start" rechnet.

Sagen wir, wir starten bei 0 und landen bei 1000 Metern Höhe: + 1000 - 0 (Steigung)

Anders herum, wir starten bei 1000 und landen bei 0 Metern Höhe: 0 - 1000 (Gefälle)

So sieht man, wie allgemein in der Mathematik üblich, schon am Vorzeichen, ob es sich um eine Steigung oder ein Gefälle handelt :-)

---

und warum -1515/31.500 ≈ -0,048095 ???
warum rechnest du nicht mit sinus und cosinus oder tangens

---

Weil in dieser Aufgabe nach der durchschnittlichen Steigung bzw. dem durchschnittlichen Gefälle gefragt ist - und nicht nach dem Steigungswinkel, der mit dem Tangens bzw. Arctan berechnet würde.