Richtung im Punkt bestimmen

Question

f(x,y)=x²+y

Es gibt eine Richtung  v = (v₁,v₂)∈ ℝ² mit ||v||₂= 1, entlang derer f im im Punkt (x,y) = (1,1) ein lokales Minimum hat.Bestimmen die diese Richtung.

Meine Rechnung:

Gradient von f(x,y)=\( \begin{pmatrix} 2x\\1 \end{pmatrix} \)

Gradient von f\( \begin{pmatrix} 1\\1\\ \end{pmatrix} \)=\( \begin{pmatrix} 2\\1\\ \end{pmatrix} \)

\( \frac{1}{||Gradient von f\begin{pmatrix} 1\\1\\ \end{pmatrix}}||\)

=\( \frac{1}{\sqrt{5}} \)·\( \begin{pmatrix} 2\\1 \end{pmatrix} \)

Was habe ich falsch gemacht?

Comments

Was mich verwirrt ist:

Hat f überhaupt irgendwo ein lokales Minimum und wenn ja wo?

Es könnte das lokale Minimum bei [0, 1] gemeint sein und dann wäre die Richtung genau [-1, 0].

Ich habe aber schon mit der Fragestellung so meine Probleme gehabt.

---

dann wäre die Richtung genau [-1, 0]
Versuche es in der Richtung   y = -2x

Was mich verwirrt ist: ||v||₂= 1

---

Dann hab ich das verkehrt verstanden und es ist schon das Minimum im Punkt (1, 1) gemeint.

Modellieren wir mal eine Gerade durch den Punkt (1, 1) mit der Steigung m wäre das

y = m·(x - 1) + 1

Setze ich das in die Ausgangsfunktion ein

f(x) = x^2 + (m·(x - 1) + 1)

Damit das ein Minimum hat, muss die Ableitung gleich null sein

f'(x) = 2·x + m = 0 --> m = - 2·x

Für x = 1 muss also m = - 2 gelten.

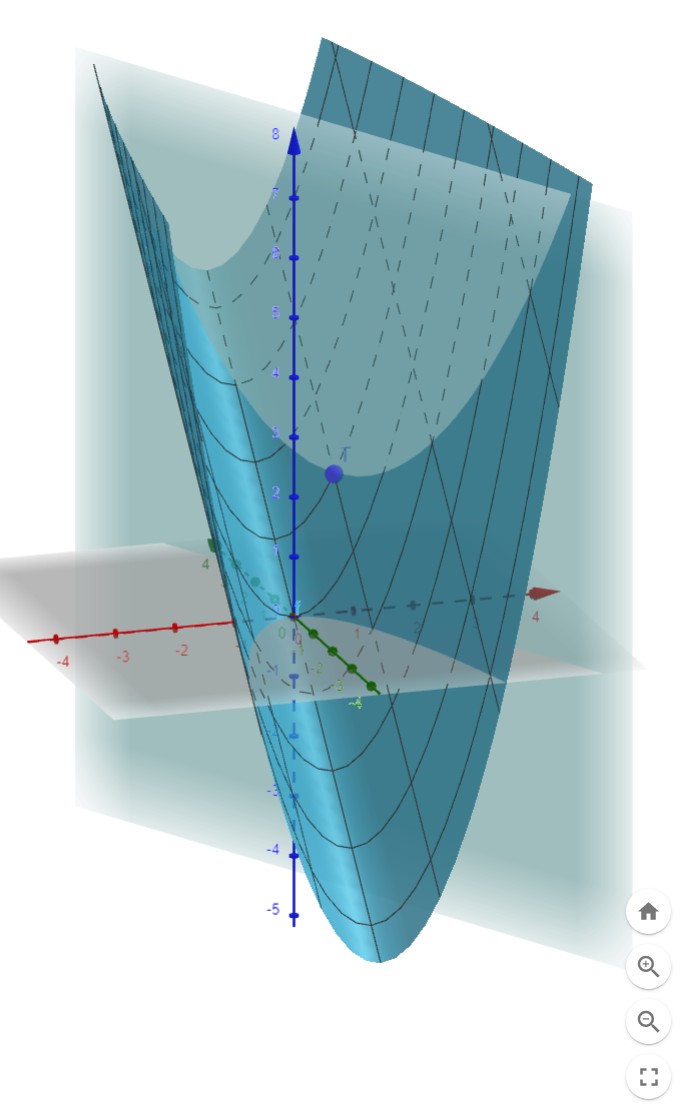
Grafisch sieht das dann wie folgt aus

Answer 1

v = (v₁,v₂)∈ ℝ² mit ||v||₂= 1

Dann ist \(v_2 = \sqrt{1 - v_1^2}\) und somit

        \(v = \begin{pmatrix}v_1\\\sqrt{1 - v_1^2}\end{pmatrix}\)

Skalarprodukt mit dem Gradienten bilden und = 0 setzen.