Integral Rechnung mathe

Question

Aufgabe:

… Integral

Problem/Ansatz:

Hallo :))

Frage 1:

Man sagt ja, wenn das Integral negativ ist, dann ist der flächeninhalt unter der x-Achse.

Bei einer Aufgabe war es jedoch so, dass  die Grenzen eines integrals vertauscht waren , jedoch der flächeninhalt über der x-Achse war. Wie kann das sein?

Frage 2:

Wenn man nur einen graphen gegeben hat, wie kommt man auf das "b" im einer quadratischen Formel?

Danke :))

Answer 1

Wenn du die Grenzen vertauscht kehrt sich auch das Vorzeichen um

∫ (b bis a) f(x) dx = - ∫ (a bis b) f(x) dx

Wenn man nur einen graphen gegeben hat, wie kommt man auf das "b" im einer quadratischen Formel?

Eine Frage wie etwa: Bestimme das b so, dass die Fläche den Wert 7 hat?

Vielleicht stellst du eine Aufgabe ein, mit der du Schwierigkeiten hast.

Comments

Das Integral ist dann negativ. Aber, wenn das Integral negativ wäre, warum ist das bei manchen Aufgaben, wo die Grenzen vertauscht wurden, der Flächeninhalt über der x-Achse.

---

Hast du ein Beispiel, damit ich das vielleicht an dem Erklären kann.

Wenn a < b gilt, dann ergibt das Integral

∫ (a bis b) f(x) dx die Flächenbilanz im Intervall [a, b] zwischen dem Graphen und der x-Achse. Hier sind Flächen unterhalb der x-Achse dann negativ.

---

Zum Beispiel bei der Funktion f(x) = -1,5x²+4,5 im Intervall von b=0 bis a=5.

---

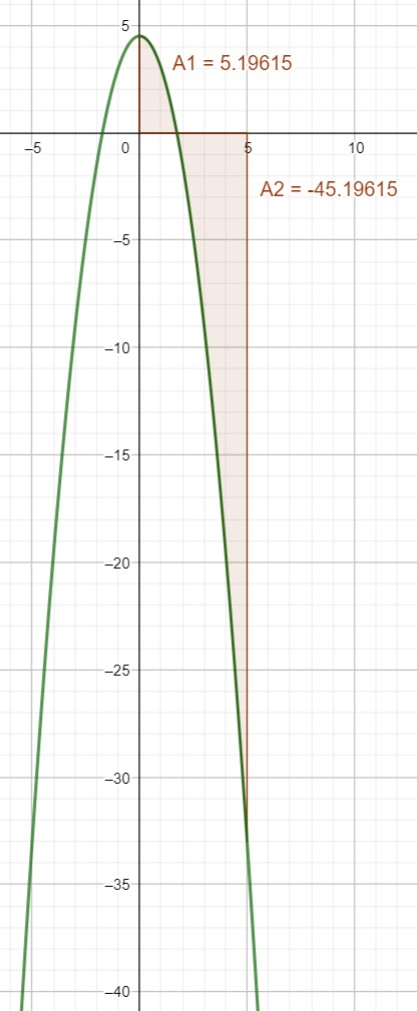
Du würdest hier über eine Nullstelle Integrieren

f(x) = 4.5 - 1.5·x²

F(x) = 4.5·x - 0.5·x³

∫ (0 bis 5) f(x) dx = F(5) - F(0) = 4.5·5 - 0.5·5³ = - 40

Hier kommt ein negativer Wert heraus, weil die Fläche unter der x-Achse sicher größer ist als die Über der x-Achse

∫ (5 bis 0) f(x) dx = F(0) - F(5) = - (4.5·5 - 0.5·5³) = 40

Hier ergibt sich die Flächenbilanz nur mit umgekehrtem Vorzeichen.

Und hier mal die gerichteten Flächeninhalte einzeln dargestellt,

---

Erstmal vielen lieben Dank.:))

Aber was wäre wenn ich die Funktion f(x)=-0,5/*5*10 hätte und von b=0 bis a=5 integrieren würde. Da wäre der integral negativ, Flächeninhalt aber über der x-Achse

---

f(x)=-0,5/*5*10

Das ist mit Sicherheit kein Funktionsterm, den du meinst.

---

Ich meinte selbstverständlich f (x)= 2x

Entschuldigung falls ich sie damit störe, aber wenn man die funktion f(x)= -0,5x²-4,5 von 0  bis 5 integriert, kommt man doch auch +40 und nicht auf -40

---

∫ (0 bis 5) 2x dx = 25 → Fläche ist über der x-Achse

Mit vertauschten Grenzen gibts ein umgekehrtes Vorzeichen. Das sollte man nicht machen.

∫ (5 bis 0) 2x dx = - 25

Entschuldigung falls ich sie damit störe, aber wenn man die funktion f(x)= -0,5x²-4,5 von 0  bis 5 integriert, kommt man doch auch +40

Du verwirrst dich nur selber, wenn du nicht mal eine Funktion ordentlich und korrekt aufschreiben kannst. Und ich kann dir dann auch nicht helfen. Sorry.