Beweise, dass für a1, a2, a3 log((a1+a2)/2)>(log(a1)+log(a2)/2

Question

Aufgabe:

Beweise, dass für a₁, a₂, a₃ > 0 folgendes gilt:

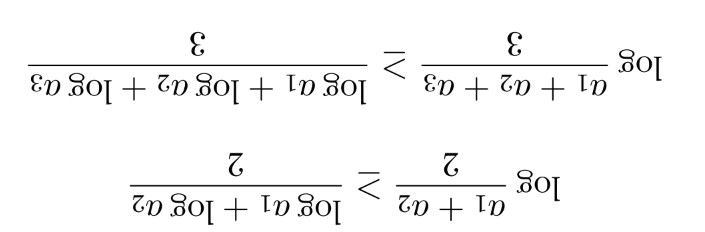
Text erkannt:

$\begin{aligned} \log \frac{a_{1}+a_{2}}{2} & \geq \frac{\log a_{1}+\log a_{2}}{2} \\ \log \frac{a_{1}+a_{2}+a_{3}}{3} & \geq \frac{\log a_{1}+\log a_{2}+\log a_{3}}{3}\end{aligned}$

Problem/Ansatz:

Das obere mit a₁ und a₂ habe ich bereits gelöst. Das sah wie folgt aus ...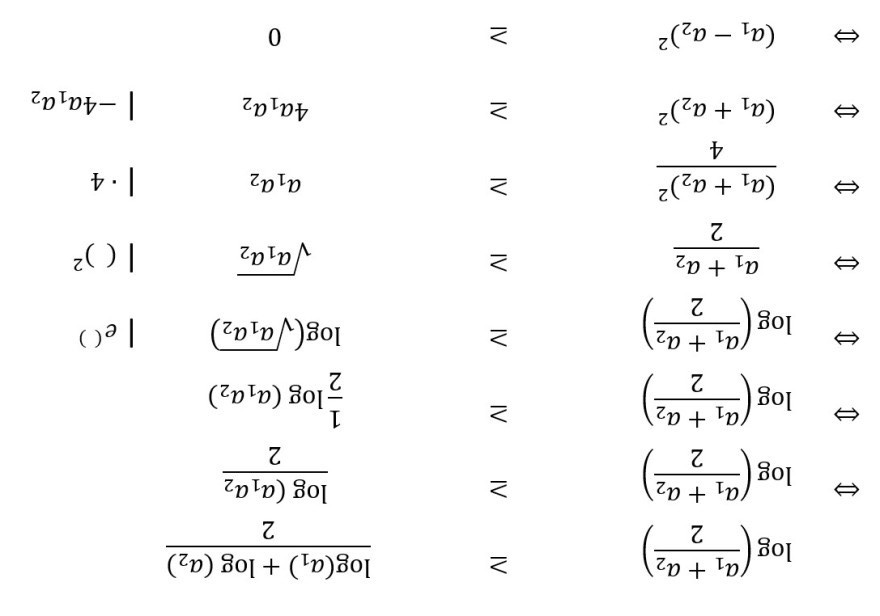

Text erkannt:

$\log \left(\frac{a_{1}+a_{2}}{2}\right) \quad \geq \frac{\log \left(a_{1}\right)+\log \left(a_{2}\right)}{2}$
$\Leftrightarrow \quad \log \left(\frac{a_{1}+a_{2}}{2}\right) \quad \geq \quad \frac{\log \left(a_{1} a_{2}\right.}{2}$
$\Leftrightarrow \quad \log \left(\frac{a_{1}+a_{2}}{2}\right) \quad \geq \quad \frac{1}{2} \log \left(a_{1} a_{2}\right)$
$\Leftrightarrow \quad \log \left(\frac{a_{1}+a_{2}}{2}\right) \quad \geq \quad \log \left(\sqrt{a_{1} a_{2}}\right) \quad \mid e^{()}$
$\Leftrightarrow \quad \frac{a_{1}+a_{2}}{2} \quad \geq \quad \sqrt{a_{1} a_{2}} \quad \mid()^{2}$
$\Leftrightarrow \quad \frac{\left(a_{1}+a_{2}\right)^{2}}{4} \quad \geq \quad a_{1} a_{2} \quad \mid \cdot 4$
$\Leftrightarrow \quad\left(a_{1}+a_{2}\right)^{2} \quad \geq \quad 4 a_{1} a_{2} \quad \mid-4 a_{1} a_{2}$
$\Leftrightarrow \quad\left(a_{1}-a_{2}\right)^{2} \quad \geq 0$

Anschließend habe ich es analog mit dem zweiten Teil machen wollen. Allerdings geht das schief, denn es kann ja sein, dass -19a₁a₂a₃ größer ist als der Rest, sodass die Ungleichung falsch wäre.

Text erkannt:

$\log \left(\frac{a_{1}+a_{2}+a_{3}}{3}\right) \quad \geq \quad \frac{\log \left(a_{1}\right)+\log \left(a_{2}\right)+\log \left(a_{3}\right)}{3}$
$\Leftrightarrow \log \left(\frac{a_{1}+a_{2}+a_{3}}{3}\right) \quad \geq \quad \frac{\log \left(a_{1} a_{2} a_{3}\right)}{3}$
$\Leftrightarrow \log \left(\frac{a_{1}+a_{2}+a_{3}}{3}\right) \quad \geq \quad \frac{1}{2} \log \left(a_{1} a_{2}\right)$
$\Leftrightarrow \quad \log \left(\frac{a_{1}+a_{2}+a_{3}}{3}\right) \quad \geq \quad \log \left(\sqrt[3]{a_{1} a_{2} a_{3}}\right) \quad \mid e^{()}$
$\Leftrightarrow \frac{a_{1}+a_{2}+a_{3}}{3} \quad \geq \quad \sqrt[3]{a_{1} a_{2} a_{3}} \quad \mid()^{3}$
$\Leftrightarrow \frac{\left(a_{1}+a_{2}+a_{3}\right)^{3}}{27} \quad \geq \quad a_{1} a_{2} a_{3} \quad \mid \cdot 27$
$\Leftrightarrow \quad \geq \quad(*) \quad 27 a_{1} a_{2} a_{3} \quad \mid-27 a_{1} a_{2} a_{3}$
$\Leftrightarrow \quad(* *) \quad \geq \quad 0$
(*) $a_{1}^{3}+a_{2}^{3}+a_{3}^{3}+3 a_{1}^{2} a_{2}+3 a_{1}^{2} a_{3}+3 a_{1} a_{2}^{2}+6 a_{1} a_{2} a_{3}+3 a_{1} a_{3}^{2}+3 a_{2}^{2} a_{3}+3 a_{2} a_{3}^{2}$
(**) $a_{1}^{3}+a_{2}^{3}+a_{3}^{3}+3 a_{1}^{2} a_{2}+3 a_{1}^{2} a_{3}+3 a_{1} a_{2}^{2}-19 a_{1} a_{2} a_{3}+3 a_{1} a_{3}^{2}+3 a_{2}^{2} a_{3}+3 a_{2} a_{3}^{2}$

Danach hab ich es nochmal etwas anders probiert, wobei ich dann nur zeigen konnte, dass zumindest die Gleichheit stimmt.

Text erkannt:

$\log \left(\frac{a_{1}+a_{2}+a_{3}}{3}\right) \geq \frac{\log \left(a_{1}\right)+\log \left(a_{2}\right)+\log \left(a_{3}\right)}{3}$
$\Leftrightarrow \log \left(\frac{a_{1}+a_{2}+a_{3}}{3}\right) \quad \geq \quad \frac{\log \left(a_{1} a_{2} a_{3}\right)}{3}$
$\Leftrightarrow \quad \log \left(\frac{a_{1}+a_{2}+a_{3}}{3}\right) \quad \geq \quad \frac{1}{2} \log \left(a_{1} a_{2}\right)$
$\Leftrightarrow \quad \log \left(\frac{a_{1}+a_{2}+a_{3}}{3}\right) \quad \geq \quad \log \left(\sqrt[3]{a_{1} a_{2} a_{3}}\right) \quad \mid e^{()}$
$\Leftrightarrow \frac{a_{1}+a_{2}+a_{3}}{3} \quad \geq \quad \sqrt[3]{a_{1} a_{2} a_{3}} \quad \mid()^{3}$
$\Leftrightarrow \frac{\left(a_{1}+a_{2}+a_{3}\right)^{3}}{27}(* * *) \quad \geq \quad a_{1} a_{2} a_{3} \quad \mid \cdot 27$
$\Leftrightarrow\left(a_{1}+a_{2}+a_{3}\right)^{3} \quad \geq \quad 27 a_{1} a_{2} a_{3} \quad 27 a_{1} a_{2} a_{3}$ für linke Seite in
$\Leftrightarrow \quad a_{1} a_{2} a_{3} \quad \geq \quad a_{1} a_{2} a_{3}$

Und jetzt weiß ich nicht mehr weiter :)

Answer 1

Das ist im Prinzip die Jensensche Ungleichung für konkave Funktionen. Also nachweisen das der Logarithmus konkav ist. Dann hast Du alles. Siehe hier

https://mathepedia.de/Jensensche_Ungleichung.html

https://de.wikipedia.org/wiki/Konvexe_und_konkave_Funktionen

Comments

Aber der erste Teil müsste doch trotzdem richtig sein?

---

Ich denke schon.