Aufgabe: Bei Aufgabe 6.c) soll die Verkettung f mit g auf Injektivität und Surjektivität untersucht werden .
Problem/Ansatz: In den Aufgabenteilen davor wurde bereits festgestellt,dass f nicht injektiv ist und g injektiv ist.
Für 0≠ y ∈ Kern(f) da ja f nicht injektiv wird in den Lösungen folgende Gleichung aufgestellt:
g(f(y)) ≠ 0(Vektor) da g inketiv ist.Müsste aber nicht g(f(y)) = 0 (Vektor) gelten, da ja y ∈ Kern(f) und somit f(y) =0 und das wiederum impliziert: g(f(y)) = g(0)=0,da der Nullvektor ja immer im Kern enhalten ist und somit auch im Kern von g enthalten ist.Also wo liegt mein Denkfehler ?
Text erkannt:
Aufgabe 6
Gegeben sei die reelle \( (3 \times 4) \)-Matrix
\( A:=\left(\begin{array}{cccc} -1 & 2 & 1 & 2 \\ 0 & 1 & 0 & -1 \\ 2 & 1 & -2 & 1 \end{array}\right) \)
(a) Die lineare Abbildung \( f: \mathbb{R}^{4} \rightarrow \mathbb{R}^{3} \) sei gegeben durch \( f(\vec{x}):=A \cdot \vec{x}, \vec{x} \in \mathbb{R}^{4} \).
(i) Bestimmen Sie eine Basis von \( \operatorname{Kern}(f) \).
(ii) Ist die Abbildung \( f \) injektiv? Ist die Abbildung \( f \) surjektiv?
(b) Die lineare Abbildung \( g: \mathbb{R}^{3} \rightarrow \mathbb{R}^{4} \) sei gegeben durch \( g(\vec{x}):=A^{T} \cdot \vec{x}, \vec{x} \in \mathbb{R}^{3} \).
(i) Bestimmen Sie die Dimension von \( \operatorname{Kern}(g) \).
(ii) Ist die Abbildung \( g \) injektiv? Ist die Abbildung \( g \) surjektiv?
(c) Ist die Abbildung \( g \circ f: \mathbb{R}^{4} \rightarrow \mathbb{R}^{4}, \vec{x} \mapsto(g \circ f)(\vec{x})=g(f(\vec{x})) \) injektiv bzw. surjektiv ?
(d) Ist die Abbildung \( f \circ g: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}, \vec{x} \mapsto(f \circ g)(\vec{x})=f(g(\vec{x})) \) injektiv bzw. surjektiv ?
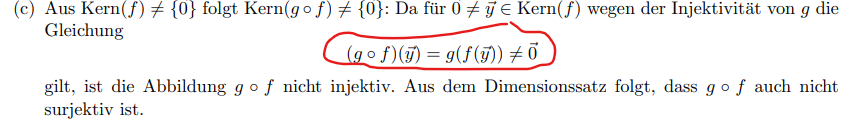
Text erkannt:
(c) Aus \( \operatorname{Kern}(f) \neq\{0\} \) folgt \( \operatorname{Kern}(g \circ f) \neq\{0\} \) : Da für \( 0 \neq \vec{y} \in \operatorname{Kern}(f) \) wegen der Injektivität von \( g \) die Gleichung
\( (g \circ f)(\vec{y})=g(f(\vec{y})) \neq \overrightarrow{0} \)
gilt, ist die Abbildung \( g \circ f \) nicht injektiv. Aus dem Dimensionssatz folgt, dass \( g \circ f \) auch nicht surjektiv ist.