Wie bestimmt man den maximalen Flächeninhalt eines trapezförmigen Kanals?

Question

Aufgabe:

Den maximalen Flächeninhalt bestimmen

Problem/Ansatz:

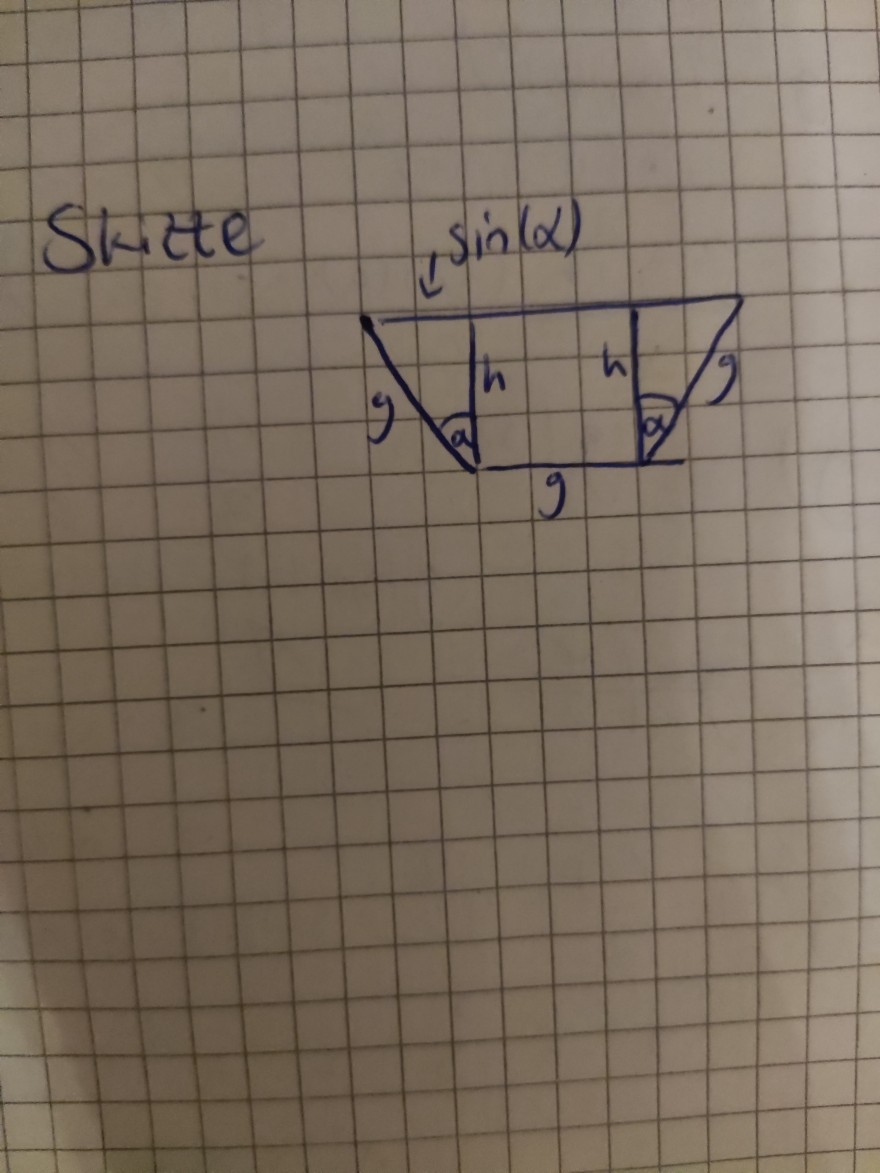
Die Formel für den Flächeninhalt habe ich schon bestimmt. Q=gh*(1+sin(a))

Die Lösung liegt auch schon vor 2x^2+x-1, x=sin(a)

Ich habe versucht das h zu definieren als h=1-sin(a)^2, analog zum Einheitskreis. Allerdings verbleibt noch das g, mit dem ich dann nichts Sinnvolles anzufangen weiß.

PS. Das Foto ist aus meinem Heft

Fehler: Dateityp „HEIC“ ist nicht erlaubt.

Comments

Ich denke mal, dass \(g\) vorgegeben ist. Oder soll das ganze in Abhängigkeit von \(g\) gelöst werden?

---

g ist nicht vorgegeben

Answer 1

SIN(α) = x/g → x = g·SIN(α)

COS(α) = h/g → h = g·COS(α)

A = 1/2·(2·x + 2·g)·h
A = 1/2·(2·g·SIN(α) + 2·g)·g·COS(α)
A = g^2·COS(α)·(SIN(α) + 1)
A' = g^2·(1 - 2·SIN(α))·(SIN(α) + 1) = 0

1 - 2·SIN(α) = 0 --> α = pi/6 = 30°

SIN(α) + 1 = 0 → Keine Lösung

Comments

Woher kommt die +1 in der dritten Spalte?

---

Woher kommt die +1 in der dritten Spalte?

es wurde \(2g\) ausgeklammert$$A = \frac{1}{2}·\underbrace{(2·g·\sin(α) + 2·g)}_{2g\cdot{\color{red}\sin(\alpha)} + 2g \cdot {\color{red}1}}·g·\cos(α)\\A =\frac{1}{2} \cdot 2g·({\color{red}\sin(α) + 1}) \cdot g \cdot \cos(\alpha)\\A = g^2·\cos(α)·({\color{red}\sin(α) + 1})$$

Answer 2

Ich zeige das mal ohne Winkel:

\(A(u,h)= \frac{1}{2}\cdot(2u+9+9) \cdot h=(u+9) \cdot h \) soll maximal werden.

\(h^2+u^2=9^2\)  →  \(h^2=9^2-u^2\)   →      \(h=\sqrt{9^2-u^2}\)

\(A(u)= (u+9) \cdot \sqrt{81-u^2}  \)

....