Gerade soll so bestimmt werden, dass Flächeninhalt des Dreiecks maximal wird.

Question

Hallo Gute-Mathe-Frage-Comunity,

ich habe ehrlich gesagt keine Ahnung wie ich die folgende Aufgabe lösen soll. Es wäre sehr nett wenn mir jemand zeigen könnte wie ich bei dieser Sorte Aufgabe vorgehen soll. Ich bin für alle Tipps offen;)

 

Hier die Aufgabe:

 

Gegeben ist eine Funktion: f(x)=(1/5)x³-16x ; und seine Normale durch den Ursprung: y=(5/16)x

 

Die Gerade mit der Gleichung x=u mit: 0 < u ≤ 4 schneidet die Normale im Punkt Q und das Schaubild K_f im Punkt P.

Zusammen mit dem Ursprung bilden diese Punkte das Dreieck OPQ.

Berechnen Sie u so, dass der Flächeninhalt de Dreiecks maximal wird. Geben Sie den maximalen Flächeninhalt an.

 

Hier habe ich euch das Gegebene schon mal aufgemalt;)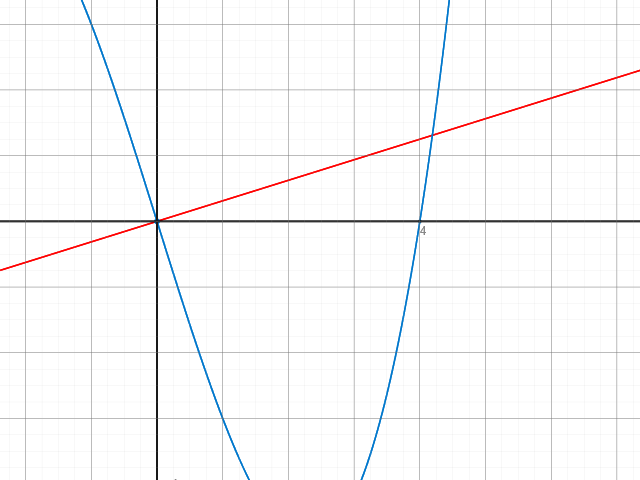

 

\left(\frac{1}{5}\right)\cdot x^3-\left(\frac{16}{5}\cdot x\right)             = f(x)=(1/5)x3-16x

 \left(\frac{5}{16}\right)\cdot x                                                             = y=(5/16)x

Ich bedanke mich jetzt schon mal für jede Hilfe.

Gruß Nick

Answer 1

f(x) = 1/5*x^3 - 16*x

g(x) = 5/16*x

Die Fläche des Dreiecks berechnet sich über 1/2 mal Grundseite mal Höhe

A = 1/2 * (g(u) - h(u)) * u = 1/2 * (5/16*u - (1/5*u^3 - 16*u)) * u = 261/32*u^2 - 1/10*u^4

Ist die Fläche maximal, dann wird die Ableitung null.

A' = 261/16*u - 2/5*u^3 = 0
u = -3√290/8 ∨ u = 3√290/8 ∨ u = 0
u = -6.386019887 ∨ u = 6.386019887 ∨ u = 0

A = 261/32*(3*√290/8)^2 - 1/10*(3*√290/8)^4 = 166.3110351