Aufgabe:
Ich soll eine Rekursion aufstellen für die Partitionszahlen. Erlaubt ist nun allerdings nur, dass jede Zahl genau einmal verwendet werden darf. Das bedeutet es gibt weniger Lösungen für die 7 zum Beispiel als ohne die Einschränkung:
Beispiel: 7 = 6+1 = 5+2 = 4+3 = 4+2+1
Es gibt also nur noch 5 Möglichkeiten die 7 darzustellen. Lösungen wie 1+1+1+1+1+1+1 gibt es dann nicht mehr.
Problem/Ansatz:
Ich habe nun die Zahlenfolge bis zur 10 ermittelt. Es ergibt sich: 1,1,2,2,3,4,5,6,8,10 (Anzahl der Möglichkeiten). Mein Problem ist aber, dass ich daraus irgenwie keine Rekursion ableiten kann. Kann mir da jemand weiterhelfen?
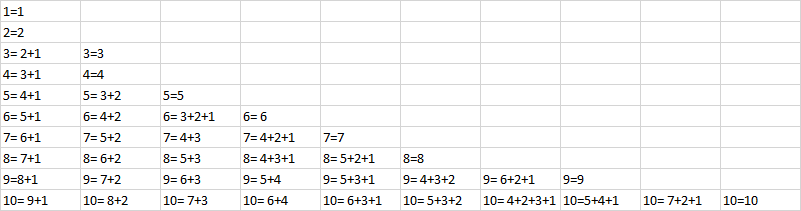
Text erkannt:
\begin{tabular}{|c|c|c|c|c|c|c|c|c|c|}
\hline \( 1=1 \) & & & & & & & & & \\
\hline \( 2=2 \) & & & & & & & & & \\
\hline \( 3=2+1 \) & \( 3=3 \) & & & & & & & & \\
\hline \( 4=3+1 \) & \( 4=4 \) & & & & & & & & \\
\hline \( 5=4+1 \) & \( 5=3+2 \) & \( 5=5 \) & & & & & & & \\
\hline \( 6=5+1 \) & \( 6=4+2 \) & \( 6=3+2+1 \) & \( 6=6 \) & & & & & & \\
\hline \( 7=6+1 \) & \( 7=5+2 \) & \( 7=4+3 \) & \( 7=4+2+1 \) & \( 7=7 \) & & & & & \\
\hline \( 8=7+1 \) & \( 8=6+2 \) & \( 8=5+3 \) & \( 8=4+3+1 \) & \( 8=5+2+1 \) & \( 8=8 \) & & & & \\
\hline \( 9=8+1 \) & \( 9=7+2 \) & \( 9=6+3 \) & \( 9=5+4 \) & \( 9=5+3+1 \) & \( 9=4+3+2 \) & \( 9=6+2+1 \) & \( 9=9 \) & & \\
\hline \( 10=9+1 \) & \( 10=8+2 \) & \( 10=7+3 \) & \( 10=6+4 \) & \( 10=6+3+1 \) & \( 10=5+3+2 \) & \( 10=4+2+3+1 \) & \( 10=5+4+1 \) & \( 10=7+2+1 \) & \( 10=10 \) \\
\hline
\end{tabular}