Hallo, kann jemand sagen wo hier der Fehler liegt?
Für Aufgabenstellung und eigene Lösung siehe Bild
Problem/Ansatz:
Ist bei 2b die Parametrisierung falsch?
Text erkannt:
2. Aufgabe: Satz von Stokes
Betrachten Sie das Vektorfeld \( v(x, y, z)=\left(2 z, x, y^{2}\right) \) und die Fläche
\( S=\left\{(x, y, z) \in \mathbb{R}^{3}: z=4-x^{2}-y^{2}, z \geq 0\right\}, \)
wobei \( \gamma=\partial S \) die Orientierung gegen den Uhrzeigersinn hat. Berechnen Sie die Zirkulation \( \oint_{\gamma}\langle v, d \vec{x}\rangle \)
a) ohne den Satz von Stokes zu benutzen.
b) mithilfe des Satzes von Stokes.

Text erkannt:
2a) \( z=4-r^{2}, r=2 \)
Fir J \( F \) is \( \sigma=2 \) und somit \( z=0 \)
1. Pravanctisierny von of
\( \gamma(t)=\left(\begin{array}{c} R \cos t \\ R \sin t \\ 0 \end{array}\right), R=2, z=0, t \in[0,2 \theta] \)
2. Tangentialvehtor
\( \gamma^{\prime}(t)=\left(\begin{array}{c} -R \sin t \\ R \cos t \\ 0 \end{array}\right) \)
3. Einsetsur conv
\( \begin{array}{l} \oint_{\gamma}^{\underline{v}} \underbrace{d \underline{x}}_{\gamma^{\prime}(t) d t}=\int \limits_{0}^{2 \pi}\left(\begin{array}{c} 0 \\ 2 \cos t \\ 4 \sin ^{3} t \end{array}\right)\left(\begin{array}{c} -R \sin t \\ R \cos t \\ 0 \end{array}\right) d t \\ =\int \limits_{0}^{2 \pi} 4 \cos ^{2} t d t .+ \\ =4 \pi \\ \end{array} \)
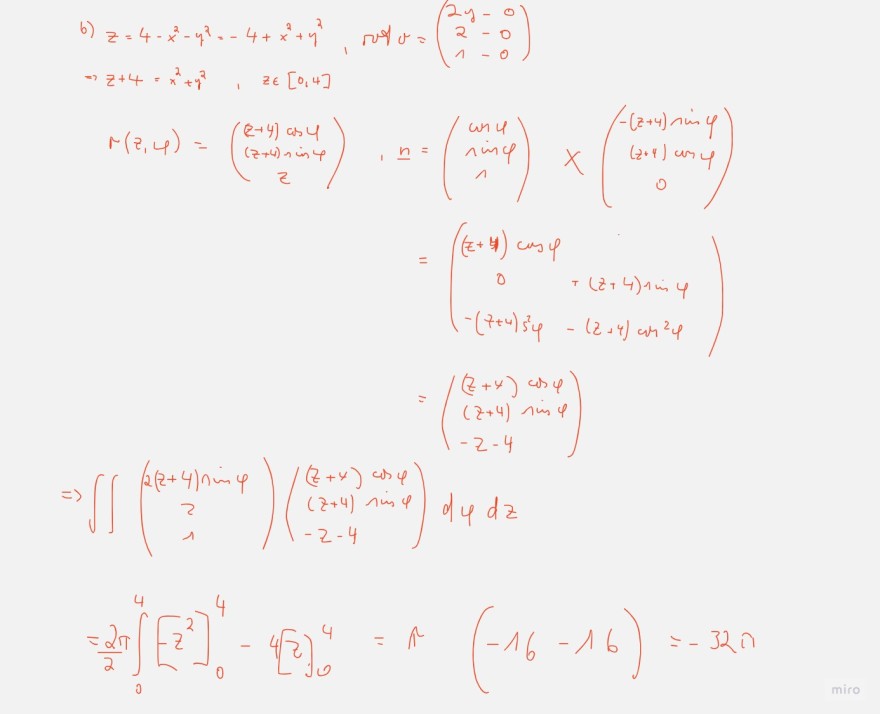
Text erkannt:
\( \begin{array}{l} \text { b) } z=4-x^{2}-y^{2}=-4+x^{2}+y^{2}, \text { तod } v=\left(\begin{array}{c} 2 y-0 \\ 2-0 \\ 1-0 \end{array}\right) \\ \Rightarrow z+4=x^{2}+y^{2}, \quad z \in[0,4] \\ r(z, \varphi)=\left(\begin{array}{c} (z+\varphi) \cos \varphi \\ (z+\varphi) \sin \varphi \\ z \end{array}\right), \underline{n}=\left(\begin{array}{c} \cos \varphi \\ \sin \varphi \\ 1 \end{array}\right) \times\left(\begin{array}{c} -(z+4) \sin \varphi \\ (z+\varphi) \cos \varphi \\ 0 \end{array}\right) \\ =\left(\begin{array}{cc} (z+y) \cos \varphi & \\ 0 & +(z+4) \sin \varphi \\ -(7+4) s^{2} \varphi & -(z+4) \operatorname{cin}^{2} \varphi \end{array}\right) \\ =\left(\begin{array}{l} (z+4) \cos \varphi \\ (z+4) \sin \varphi \\ -z-4 \end{array}\right) \\ \Rightarrow \iint\left(\begin{array}{c} 2(z+4) \sin \varphi \\ 2 \\ 1 \end{array}\right)\left(\begin{array}{c} (z+4) \cos \varphi \\ (z+4) \sin \varphi \\ -z-4 \end{array}\right) d \varphi d z \\ =\frac{2 \pi}{2} \int \limits_{0}^{4}\left[-z^{2}\right]_{0}^{4}-4[z]_{0}^{4}=\pi(-16-16)=-32 \pi \\ \end{array} \)
miro