Taylorpolynom bestimmen und Restglied abschätzen

Question

Hallo, ich sollte folgendes machen:

Aufgabe:

Sei f(x) = ln(1 + x), die Funktion.

Bestimme das Taylorpolynom Grad 2 für den Entwicklungspunkt p = 2 und schätze den Fehler für x aus [1,3] ab.

1) Das Taylorpolynom:

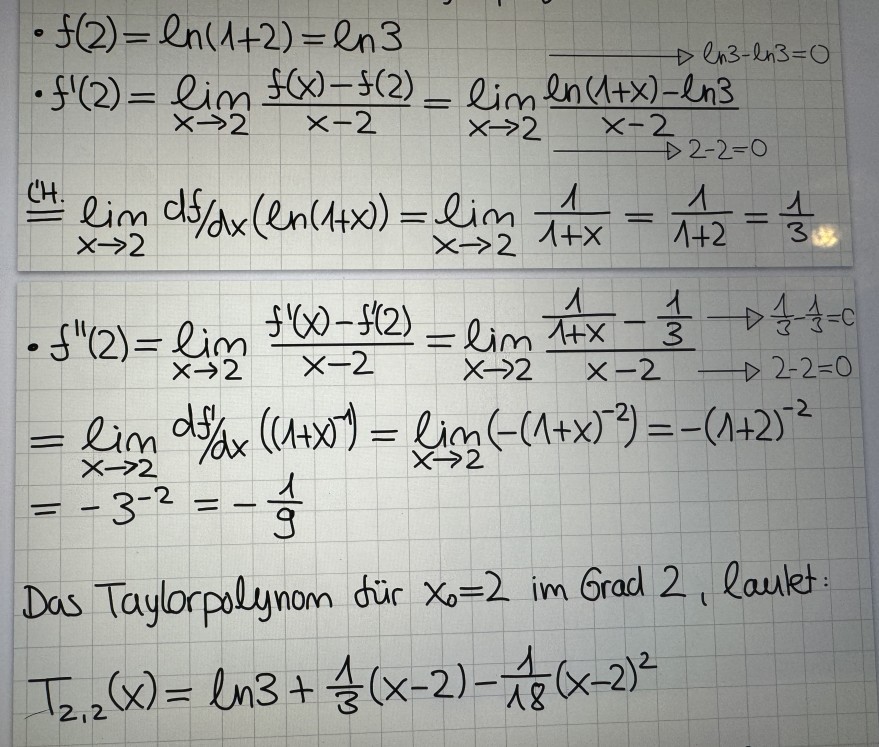
Text erkannt:

$\begin{array}{l} \text { - } f(2)=\ln (1+2)=\ln 3 \\ \text { - } f^{\prime}(2)=\lim \limits_{x \rightarrow 2} \frac{f(x)-f(2)}{x-2}=\lim \limits_{x \rightarrow 2} \frac{\ln (1+x)-\ln 3}{x-2} \ln 3=0 \\ \text { ('H. } \lim \limits_{x \rightarrow 2} d f / d x(\ln (1+x))=\lim \limits_{x \rightarrow 2} \frac{1}{1+x}=\frac{1}{1+2}=\frac{1}{3} \\ \text { - } f^{\prime \prime}(2)=\lim \limits_{x \rightarrow 2} \frac{f^{\prime}(x)-f^{\prime}(2)}{x-2}=\lim \limits_{x \rightarrow 2} \frac{\frac{1}{1+x}-\frac{1}{3} \longrightarrow \frac{1}{3}-\frac{1}{3}=c}{x-2} \longrightarrow 2-2=0 \\ =\lim \limits_{x \rightarrow 2} d f^{\prime} / d x\left((1+x)^{-1}\right)=\lim \limits_{x \rightarrow 2}\left(-(1+x)^{-2}\right)=-(1+2)^{-2} \\ =-3^{-2}=-\frac{1}{9} \end{array}$

Das Taylorpolynom dür $x_{0}=2$ im Grad 2, laulet:
$T_{2,2}(x)=\ln 3+\frac{1}{3}(x-2)-\frac{1}{18}(x-2)^{2}$

2) Der abgeschätzte größtmögliche Fehler

Text erkannt:

2. Schritt: Bilde die dritte Ableitung $f^{\prime \prime \prime}$ von $f$ :
$f^{\prime \prime \prime}(x) \stackrel{a}{=} \frac{2}{(1+x)^{3}}$
3. Schritt: Schäta den Fehler dür $x \in[1,3] a b$ : Nach dem Satz von Taylor $\exists x_{1} \in(x, 2) \cup(2, x)$, sodass: $f(x)=T_{2,2}(x)+f^{\prime \prime \prime}\left(x_{1}\right) \frac{(x-2)^{3}}{3 !}$. Also gilt damit: $\left|f(x)-T_{2,2}(x)\right|=\left|f^{\prime \prime \prime}\left(x_{1}\right) \frac{(x-2)^{3}}{3 !}\right|$.
Für $x \in[1,3]$ ist $x \leq 3$, also $x-2 \leq 1$ \& somit $(x-2)^{3} \leq$ $1^{3}=1$. Außerdem gilt $\left|f^{\prime \prime \prime}\left(x_{1}\right)\right|=\frac{2}{\left(1+x_{1}\right)^{3}} \leq \frac{2}{(1+1)^{3}}=\frac{2}{8}$ $=\frac{1}{4}$. Insgesamt folgt: $\underbrace{(1+1)^{3}}_{=2^{3}=8}$
$\begin{array}{l} \left|f(x)-T_{2,2}(x)\right|=\left|f^{\prime \prime \prime}\left(x_{1}\right) \frac{(x-2)^{3}}{3 !}\right|=\left|f^{\prime \prime \prime}\left(x_{1}\right)\right| \frac{\left|(x-2)^{3}\right|}{6} \\ \leqslant \underbrace{\left|f^{\prime \prime \prime}\left(x_{1}\right)\right|}_{\geqslant 0} \frac{1}{6}=\frac{2}{\left(1+x_{1}\right)^{3}} \cdot \frac{1}{6} \leqslant \frac{1}{4} \cdot \frac{1}{6}=\frac{1}{24} . \end{array}$

———-

Hab ich das alles richtig gemacht? Ich würd mich auf eine Meinung freuen.

Comments

Mir erschließt sich nicht, warum du jedes mal die Differenzialquotienten aufschreibst, wenn du die Ableitungen von ln(1+x) und (1+x)^-n sowieso nach den bekannten Ableitungsregeln bildest.

Das Taylorpolynom selbst ist richtig.

---

Ja stimmt, kann es auch einfach dann einsetzen und den Wert bestimmen. Okay das freut mich schon mal, das das Polynom korrekt ist. Ist denn auch der zweite Teil der Aufgabe, mit der Restglied abschätzung so richtig?

---

Da die Reihenentwicklung alterniert

$\log (3)+\frac{x-2}{3}-\frac{1}{18}(x-2)^{2}+\frac{1}{81}(x-2)^{3}-\frac{1}{324}(x-2)^{4}+\frac{(x-2)^{5}}{1215}-$

ist bereits das Glied mit der 3. Potenz eine noch schärfere Abschätzung. Der Fehler kann maximal $\frac{1}{81}(x-2)^{3}$ sein, was an den Intervallgrenzen 1 und 3 jeweils 1/81 ergibt.

Aber vermutlich sollt ihr das Restglied so wie du abschätzen.

---

Dankeschön! :)

Answer 1

Ja, ist alles richtig so. Aber eine Kleinigkeit: Du musst $|x-2|^3$ abschätzen, nicht $(x-2)^3$. Kommt aber auch auf 1 raus. Außerdem solltest noch begründen, dass $f'''(x)$ auf [1,3] positiv ist. Ich hab den Eindruck Du hast generell nicht dran gedacht, dass die Beträge abgeschätzt werden müssen.

Und zu den Ableitungen ist ja schon was gesagt worden. Wenn man die Ableitung von $\ln$ kennt (und die musst Du für l'H auch kennen), geht das ganz flott.

Comments

Super, ich danke euch allen! :)