Bestimmen Sie jeweils die Wahrscheinlichkeitsverteilung der Zufallssgröße X: Anzahl der Runden bis zum Spielende …

Question

Aufgabe:

Bei einem Spiel werden Kugeln aus einer Urne mit 5 schwarzen und 1 weißen Kugel gezogen. Das Spiel ist beendet, wenn die weiße Kugel gezogen wurde, spätesten jedoch nach der 5. Ziehung.

Es wird (1) mit zürucklegen und (2) ohne zurücklegen gezogen.

a) Bestimmen Sie jeweils die Wahrscheinlichkeitsverteilung der Zufallssgröße X: Anzahl der Runden bis zum Spielende sowie den Erwartungswert der Zufallsgröße.

Problem/Ansatz:

Ansatz habe ich hoch geladen. Mein Problem liegt nur darin, dass mein P(X=x;) nicht 1 ergibt. Ich habe entlang der Pfade gerechnet -> zum Beispiel ist ja ab der zweiten Runde vorbei, wenn man beim ersten Mal 5/6 (schwarz) und danach 1/6 also weiß zieht und so kommt entsprechend 5/36 zustande. Usw.

Würde mich über eine Korrektur freuen.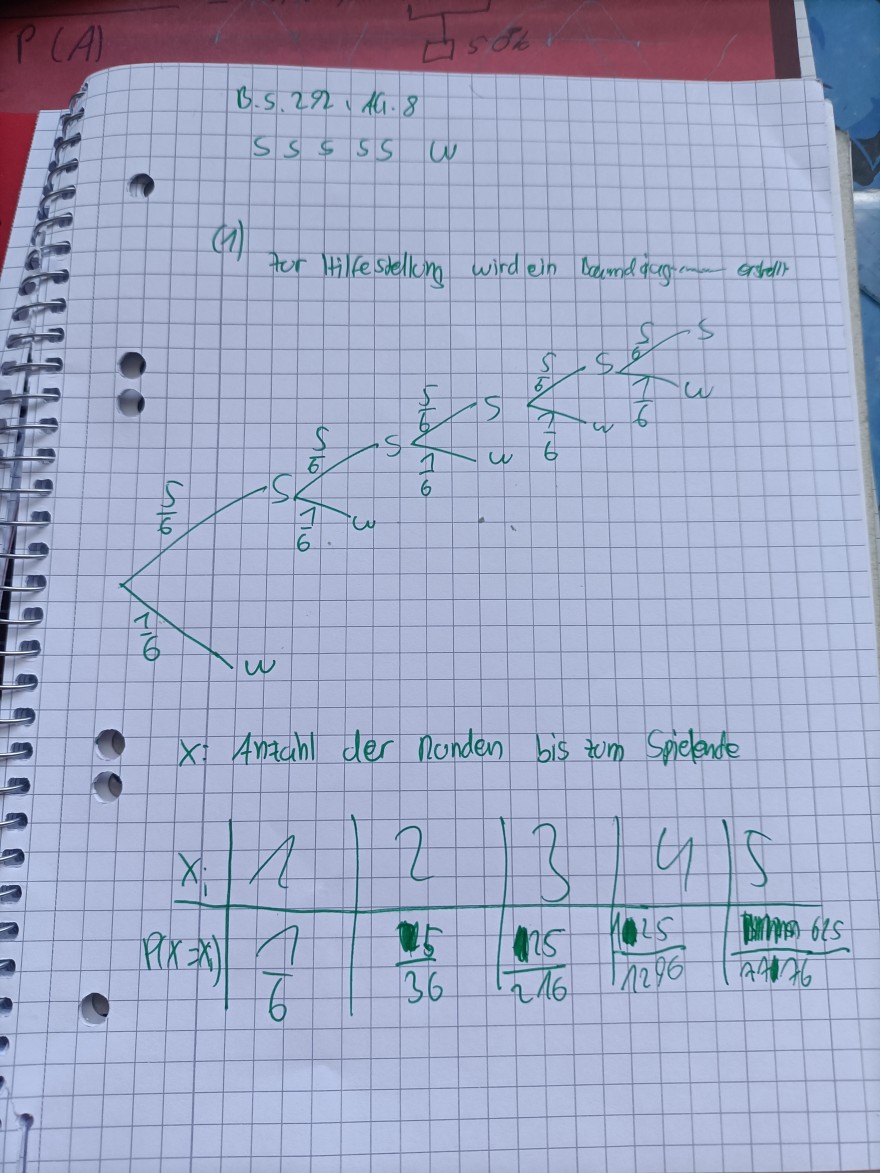

Text erkannt:

\( \begin{array}{l} \text { B. } 5.292 \text {. AG. } 8 \\ 55555 \mathrm{w} \end{array} \)
(1) For Hilfestellung wird ein boundaiag asmell.

X: Anzahl der nunden bis zum Spielente
\begin{tabular}{c|c|c|c|c|c}
\( x_{i} \) & \( A \) & 2 & 2 & 0 & \( \int \) \\
\hline\( P(x=x) \) & \( \Lambda \) & \( \frac{15}{36} \) & \( \frac{125}{216} \) & \( \frac{125}{1296} \) & \( \frac{1}{14176} \)
\end{tabular}

Comments

Warum sollte 1 rauskommen, wenn nicht zurückgelegt wird?

Die weiße kann auch nie gezogen werden.

---

Dem FS geht es um die Summe der Wahrscheinlichkeiten, die bei ihm nicht 1 ergibt, weil er einen Pfad vergessen hat. Darüber hinaus geht es hier noch um den Fall mit Zurücklegen und nicht ohne Zurücklegen. Und auch wenn die weiße Kugeln im zweiten Fall nicht gezogen werden kann, endet das Spiel nach 5 Runden.

---

@ggT22, MC: Es ist wirklich super, dem FS die komplette Lösung vorwegzunehmen, wenn es offenbar nur um einen Denkfehler geht. Richtig klasse! Den Rest hätte er sicherlich alleine hinbekommen!

---

Ich schreibe meine Lösung hin, damit alle, die sich wie ggT22 an der Aufgabe probieren wollen, eine Lösung zum Vergleich haben.

Und natürlich auch damit ich ein Feedback habe, ob ich einen Denk- oder Rechenfehler gemacht habe.

Ich bezweifle nicht, dass der Fragesteller es auch ohne meine Lösung hinbekommt. Allerdings finde ich es nützlich, am Ende eine Vergleichslösung zu haben.

Du musst es aber nicht verstehen, wenn du nicht willst.

---

Ich ging davon aus, dass man spätestens bei 5.Zug trifft.

---

Selbst dann wäre die Wahrscheinlichkeit für den letzten Zug 1, wenn man mit Sicherheit trifft.

Answer 1

a1)

P(X = 1) = 1/6
P(X = 2) = 5/6·1/6 = 5/36
P(X = 3) = (5/6)^2·1/6 = 25/216
P(X = 4) = (5/6)^3·1/6 = 125/1296
P(X = 5) = (5/6)^4 = 625/1296

E(X) = 1·1/6 + 2·5/36 + 3·25/216 + 4·125/1296 + 5·625/1296 = 4651/1296 = 3.589

a2)

P(X = 1) = 1/6
P(X = 2) = 5/6 * 1/5 = 1/6
P(X = 3) = 5/6 * 4/5 * 1/4 = 1/6
P(X = 4) = 5/6 * 4/5 * 3/4 * 1/3 = 1/6
P(X = 5) = 5/6 * 4/5 * 3/4 * 2/3 = 2/6

E(X) = 1·1/6 + 2·1/6 + 3·1/6 + 4·1/6 + 5·2/6 = 10/3 = 3.333

Comments

Danke für die sehr ausführliche Antwort.

Answer 2

Das Spiel endet auch, wenn du 5 mal die schwarze Kugel gezogen hast. Diesen Pfad hast du bei der Wahrscheinlichkeit, dass das Spiel nach 5 Zügen endet, vergessen.

Comments

Danke sehr für den tollen Tipp

Answer 3

ohne Zurücklegen: hypergeometrische Verteilung:

P(X=1) = 1/6

P(X=2) = 5/6*1/6

P(X=3) = 5/6*4/5*1/4

P(X=4) ) 5/6*4/5*3/4*1/3

P(X=5) = 5/6*4/5*3/4*2/3*1/2

Comments

P(X = 5) ist meiner Meinung nach nicht richtig.

---

Ist es auch nicht, weil es beim letzten Zug egal ist, was man zieht, da das Spiel so oder so endet.