Berechnen Sie \operatorname{det} A durch Entwicklung nach der 3.

Question

Kann mir jemand sagen, woher das 2. minus vor der Determinante kommt:

Text erkannt:

(a) Berechnen Sie $\operatorname{det} A$ durch Entwicklung nach der 3. Spalte. (Hinweis: Sie können vorher die 3. Spalte durch eine Zeilenumformung vereinfachen.)
(b) Entscheiden Sie mithilfe der Determinante, ob die Matrix $B$ invertierbar ist. Berechnen Sie in diesem Fall $B^{-1}$.
(17)
$\operatorname{det} A=\operatorname{det}\left(\begin{array}{cccc} 1 & 2 & 0 & 1 \\ 1 & -2 & -1 & -1 \\ 2 & -2 & 0 & 1 \\ 0 & -6 & -3 & 1 \end{array}\right)_{-3 I}=\operatorname{det}\left(\begin{array}{cccc} 1 & 2 & 0 & 1 \\ 1 & -2 & -1 & -1 \\ 2 & -2 & 0 & 1 \\ -3 & 0 & 0 & 4 \end{array}\right)$
(2P)
(2P)
$=-(-1) \cdot \operatorname{det}\left(\begin{array}{ccc} 1 & 2 & 1 \\ 2 & -2 & 1 \\ -3 & 0 & 4 \end{array}\right)_{/ 2 p}=+(\underbrace{-8-6-6-16}_{-20})=\underline{L}_{2 p}^{-36}$

Answer 1

Wer hat das gerechnet, wo ist denn Deine Rechnung?

Das minus ist das übliche aus dem Entwicklungssatz.

Comments

Ich habe es auch mit dem Entwicklungssatz gemacht, allerdings kommt nur ein Minus bei mir:

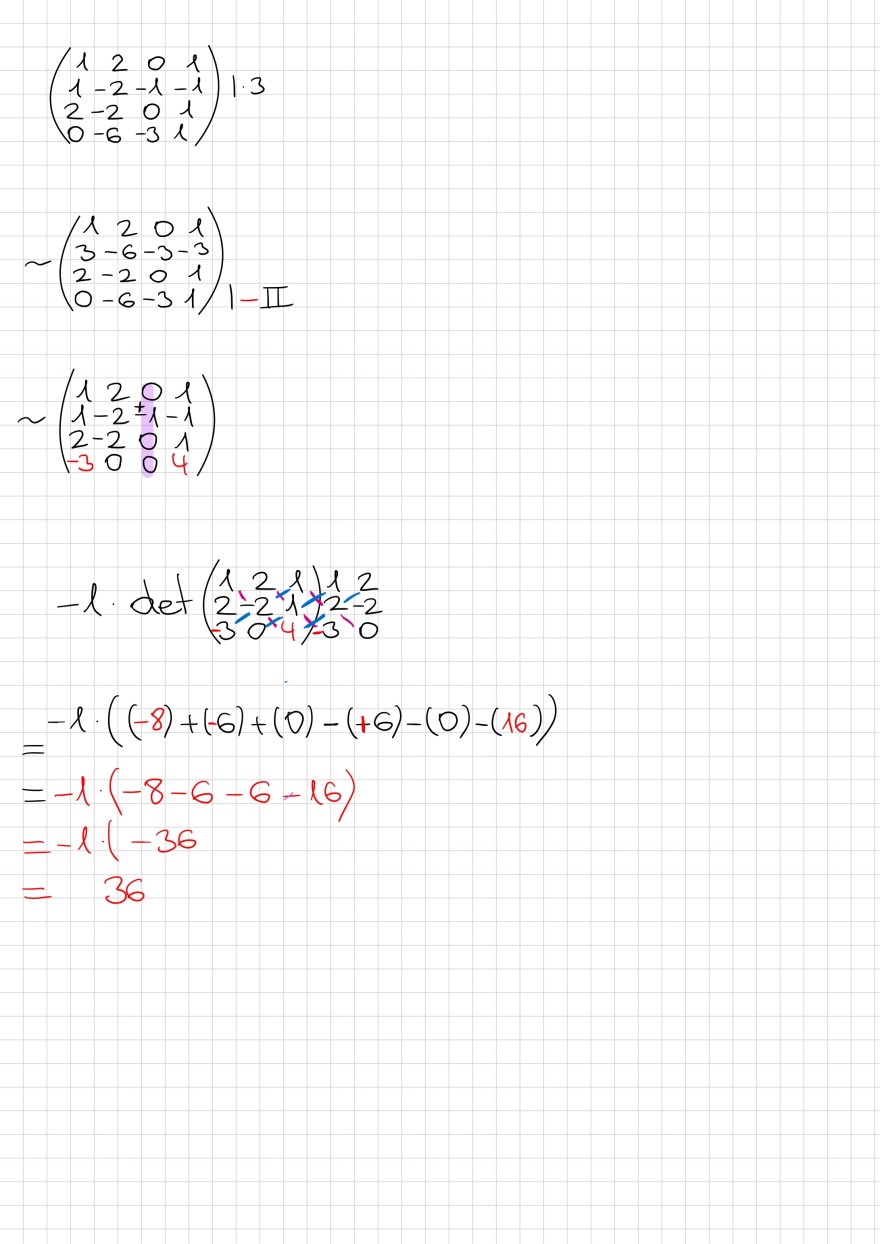
Text erkannt:

$\begin{array}{l} \left.\left(\begin{array}{cccc} 1 & 2 & 0 & 1 \\ 1 & -2 & -1 & -1 \\ 2 & -2 & 0 & 1 \\ 0 & -6 & -3 & 1 \end{array}\right) \right\rvert\, \cdot 3 \\ \sim\left(\begin{array}{cccc} 1 & 2 & 0 & 1 \\ 3 & -6 & -3 & -3 \\ 2 & -2 & 0 & 1 \\ 0 & -6 & -3 & 1 \end{array}\right) 1-I I \\ \sim\left(\begin{array}{cccc} 1 & 2 & 0 & 1 \\ 1 & -2 & 1 & 1 \\ 2 & -1 \\ -3 & 0 & 0 & 1 \\ -3 & 0 & 4 \end{array}\right) \\ -l \cdot \operatorname{det}\left(\begin{array}{llll} 1 & 2 & 1 \\ 2 & -1 & 1 & 1 \\ 2 & -2 & 1 \\ -3 & 0 \times 4 & -2 & -2 \\ 0 \end{array}\right. \\ =-l \cdot((-8)+(-6)+(0)-(+6)-(0)-(16)) \\ =-1 \cdot(-8-6-6-16) \\ =-l \cdot(-36 \\ =36 \end{array}$

---

Zeile "mal 3" ist keine(!) zulässige Umformung bei der Det-Bestimmung. Du hast danach wieder "durch 3" gerechnet, dadurch entstand kein Fehler.

Ansonsten beachte weiterhin den Tipp von user26605 zu den Vorzeichen um nicht durcheinander zu kommen. Der Tipp galt generell(!), nicht nur für die vorherige Frage.

Answer 2

Es wurde nach der 3. Spalte entwickelt. Da stehen drei Nullen drin und der bewusste Eintrag -1.

Comments

Ouh ja hab da ein Plus statt ein Minus hingeschrieben, vielen Dank