Grenzwertregel bei Folgen

Question

Seien (a_n) und (b_n) zwei reelle nicht negative Folgen, die beide konvergieren a_n —> a > 0 und b_n —> b > 0 für n gegen unendlich.

Falls a_n ≥ b_n für alle n ≥ 1 gilt, folgt dann auch die Ungleichung a ≥ b_n für alle n ≥ 1 ?

Comments

Nein, gefühlsmäßig würde ich sagen, dass stimmt nicht. Ein Gegenbeispiel sollte reichen:

a_n = 1+\( \frac{2}{n} \)

b_n = 1+\( \frac{1}{n} \)

Grenzwert a=b=1

a_n>b_n

Aber b_n > 1=a

---

Danke sehr kompakt!

Answer 1

Die Aussage ist falsch. Siehe folgendes Gegenbeispiel:

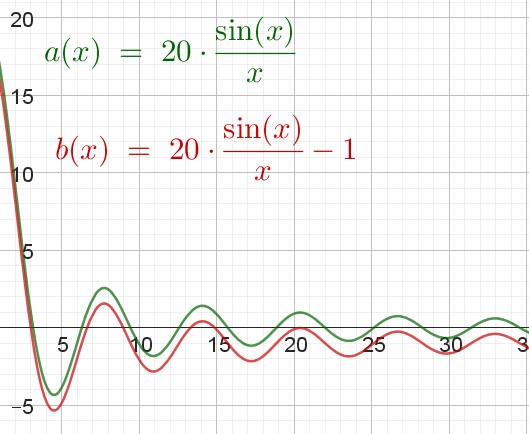
Das sind zwar keine Zahlenfolgen, sondern für alle x definierte Funktionen, aber du kannst dir ja die Werte für nicht ganzzahlige Argumente wegdenken.

Es gilt immer a(x)>b(x).

a(x) konvergiert gegen 0, es gibt aber Werte von b, die grö0er als 0 sind.

Comments

Danke sehr für das ausführliche Gegenbeispiel!