Periodische Vorgänge modellieren

Question

Aufgabe:

Die Pista di Nardò ist eine kreisförmige Autoteststrecke in
Italien mit einem Durchmesser von 4km. Den Abstand
eines Autos vom Startpunkt in einer Runde kann man
durch eine Sinusfunktion beschreiben.
a) Ein Auto benötigt für eine Runde 5,4 Minuten. Stelle
eine Funktionsgleichung für den Abstand des Autos
vom Startpunkt auf.
b) Ein anderes Auto fährt mit 190km/h über die Test-
strecke. Stelle eine passende Funktionsgleichung für
dieses Auto auf und berechne, wann es genau 2km
vom Startpunkt entfernt ist.
c) Ein drittes Auto dreht mehrere Runden mit 240km/h auf der Strecke. Berechne, wie
weit es nach 10 Minuten vom Startpunkt entfernt ist.

Problem/Ansatz

Ich verstehe wirklich garnichts

Comments

Man müßte sich wohl erst einmal überlegen, was denn mit Abstand vom Startpunkt genau gemeint ist. Ich finde die Aufgabenstellung nicht präzise.

Hier ein Skizze, eine LE entspricht 1km.

Das Fahrzeug bewege sich vom Startpunkt S im Gegenuhrzeiger-Sinn (mathematisch positiv) auf der Kreisbahn.

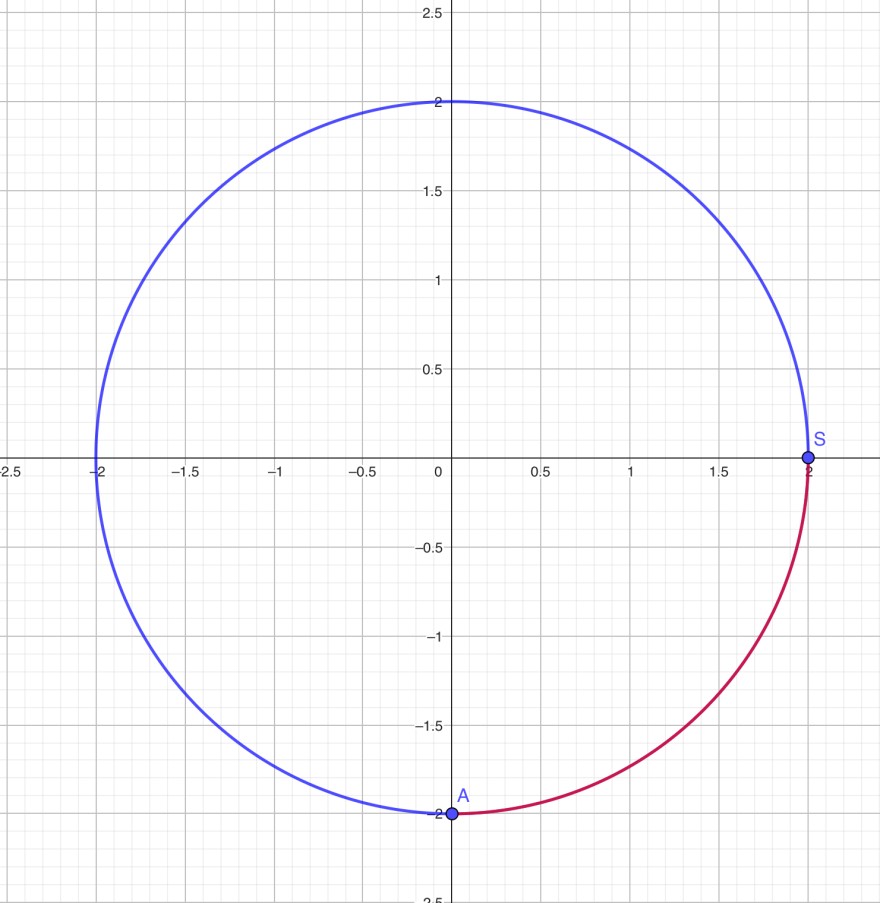
Was genau ist nun mit Abstand gemeint?

Wenn es die gefahrene Strecke auf der Kreisbahn wäre, dann ist diese keine Sinusfunktion da die Strecke (=Bogenlänge) linear von der (angenommenen konstanten) Geschwindigkeit abhängt. Das ist dann wohl nicht gemeint.

Wenn aber mit Abstand, z.B. wenn es bei Punkt A angekommen ist, nicht die bisher gefahrene Strecke (also der blaue dreiviertel Kreisumfang) sondern der viertel Kreisumfang (also die noch zu fahrende Rote Strecke) gemeint wäre, dann wäre das tatsächlich eine periodische Funktion.

Wenn aber die Entfernung per Luftlinie gemeint ist (Euklidischer Abstand = die Länge der Sehne), dann ergibt sich auch wieder eine periodische Funktion. Ich vermute, diese wird hier gemeint sein.

---

Ich vermute, diese wird hier gemeint sein

Die Vermutung kannst du leicht selbst durch den Nachweis des sinusförmigen Verlaufs dieser Strecke (da ist die Aufgabenstellung übrigens völlig eindeutig) bestätigen.

---

Das ich das kann ist nicht der Punkt. Hier geht es (vermutlich) um eine Aufgabe für Schüler, die diese Gedankengänge auch durchführen müßten. Eine eindeutigere Aufgabenstellung wäre somit wünschenswert.

offtopic: wenn ich mit meinem Porsche auf der Rennstrecke unterwegs bin, interessiert nur die Rundenzeit, höchstens noch die gefahrene Strecke aber nie der Euklidische Abstand zu Start/Ziel ;-)

---

wenn ich mit meinem Porsche ...

Döschwofahren. Viele fühlen sich berufen, doch nicht jeder ist auserwählt.

(ich fahre übrigens nicht Döschwo, aber wurde öfteres damit gefahren - der Unterschied ist, wenn man Bananen verschnapsen tut, dann fährt damit ein Döschwo, aber ein Porsche nicht, aus snobismusstrategischen Gründen)

---

So eine Ente hatte ich als Student, war damals cool, zumindest dachte man das…

Answer 1

Eine Skizze ist ein guter Anfang: Kreis mit Startmarkierung.

Für a) beginne mit einer Wertetabelle für die Funktion f(t) = Abstand vom Startpunkt (in km) zum Zeitpunkt t (in Min.). Was ist f(0), f(5.4), f(10.8), f(2.7)? Finde damit f(t) allgemein aus.

b) geht fast genauso, berechne erst die Fahrzeit für eine Runde, weiter wie in a).

Die Idee solcher Aufgaben zu lernen sich die math. Zusammenhänge aus dem Text zu erarbeiten. Das lernt man nicht durch Lesen fertiger Lösungen, sondern durch selbst ausprobieren. Dass man am Anfang gar nichts erkennt, ist in den ersten Sekunden nach dem Durchlesen normal.

Answer 2

a)

In 5,4 Minuten = 324 Sekunden legt das Fahrzeug einen Winkel φ von 360 Grad um den Mittelpunkt des Kreises (mit Radius r = 2000 Meter) herum zurück.

Die Polarkoordinaten des Autos (φ, Radius) können umgerechnet werden in kartesische Koordinaten (r cos φ│r sin φ), wobei φ(t) = 360° * t/324.

Die euklidische Distanz zwischen Standort und Startpunkt ist somit

\(\displaystyle d(t)= \sqrt{\left(2000 \cdot\cos(360^{\circ} \cdot t/324)-2000\right)^2+\left(2000 \cdot \sin(360^{\circ} \cdot t/324)-0\right)^2} \)

\(\displaystyle \quad \; = 4000 \cdot │\sin\left(\frac{t}{324}\cdot 180^{\circ}\right)│ \)

Comments

Vielleicht wären Beträge nicht verkehrt - ok, geht doch :-)

---

Ja klar, danke für den porscheschnellen Hinweis.

https://maps.app.goo.gl/fLjzmKoLTJhfk4Py5

@ Jennifer2aer: Mit meiner Antwort wird gezeigt, dass es tatsächlich eine Sinusfunktion ist. Man kann stattdessen auch einfach ein paar Punkte ausrechnen, dem Aufgabenautor glauben dass es ein Sinus ist, und die Sinuskurve dann an die Punkte anpassen. So haben es andere Antwortgeber hier getan. Und sind auf dieselbe Funktion gekommen (allerdings mit Kilometer anstatt Meter und mit Minuten anstatt Sekunden).

---

Cooles Teil! Kannte ich nicht.

War ursprünglich als "Basis eines Teilchenbeschleuigers" geplant (Wikipedia).

Answer 3

Die Pista di Nardò ist eine kreisförmige Autoteststrecke in Italien mit einem Durchmesser von 4 km. Den Abstand eines Autos vom Startpunkt in einer Runde kann man durch eine Sinusfunktion beschreiben.

a) Ein Auto benötigt für eine Runde 5.4 Minuten. Stelle eine Funktionsgleichung für den Abstand des Autos vom Startpunkt auf.

Offensichtlich gilt:

d(0) = d(5.4) = 0 km
d(2.7) = 4 km
d(1.35) = d(4.05) = √(2² + 2²) ≈ 2.828 km

Skizze

~plot~ 4*sin(pi/5.4*x);{0|0};{1.35|2.828};{2.7|4};{4.05|2.828};{5.4|0};[[-0.1|5.5|-0.1|4.1]] ~plot~

Beachte, dass der Definitionsbereich nur [0, 5.4] ist, weil die Funktion für den Abstand in einer Runde gilt. Will man die Funktion für den Abstand in mehreren Runden haben, müsste man den Betrag dieser Funktion nehmen.

Comments

Hier nur meine Ergebnisse für b) & c) zum Vergleich.

b) Ein anderes Auto fährt mit 190 km/h über die Teststrecke. Stelle eine passende Funktionsgleichung für dieses Auto auf und berechne, wann es genau 2 km vom Startpunkt entfernt ist.

d2(x) = 4·SIN(19/24·x) = 2 → x ≈ 39.68 s ∨ x ≈ 3 min 18.42 s

c) Ein drittes Auto dreht mehrere Runden mit 240 km/h auf der Strecke. Berechne, wie weit es nach 10 Minuten vom Startpunkt entfernt ist.

d3(10) = 4·|SIN(10)| ≈ 2.176 km