Ich geb dir mal an, wie du anfangen kannst und vermute, dass du nun selbst weiterkommst.
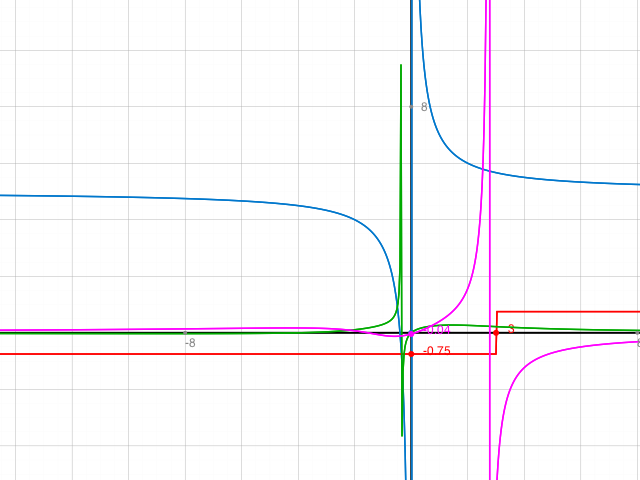
Um eine erste Übersicht zu erhalten, kann man die Graphen der Funktionen aufzeichnen.
Hier siehst du, dass sich a) (violett) für x --> minus unendlich einer kleinen Zahl annähert.
b) (grün) ist an der Stelle x=0 anscheinend stetig. (Definitionslücke) scheint hebbar (d.h. sollte sich rauskürzen lassen).
c) (blau) hat offensichtlich an der Stelle x=0 eine Unstetigkeitsstelle. Also: zeigen, dass der Grenzwert nicht existiert.
d) (rot) springt an der Stelle x=3. Also: Zeige mit einer Fallunterscheidung (1. Fall x<3 und 2. Fall x>3), dass der Grenzwert von links und rechts dort unterschiedlich sind.